- Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm:
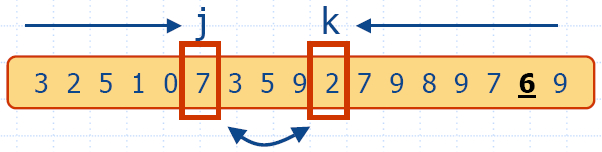
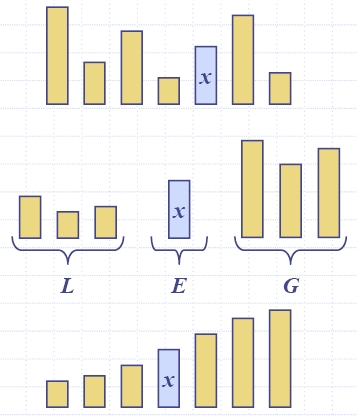
- Divide: pick a random element x (called pivot) and partition S into
- L elements less than x
- E elements equal x
- G elements greater than x
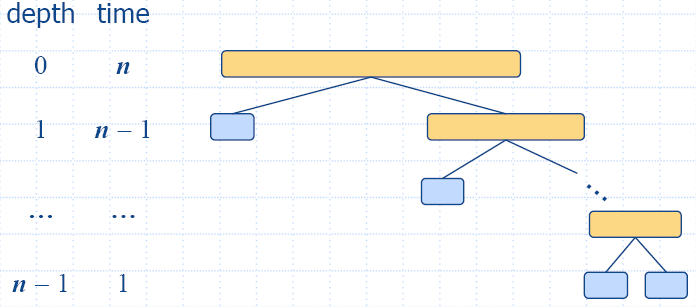
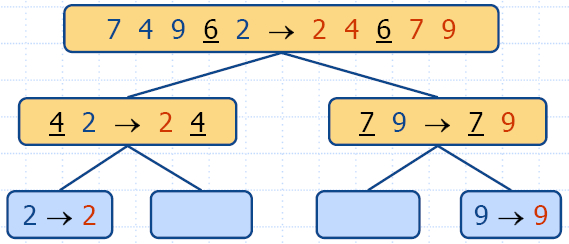
- Recur: sort L and G
- Conquer: join L, E and G