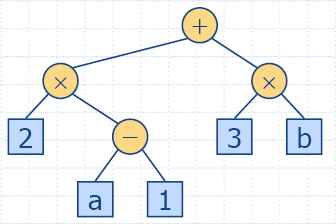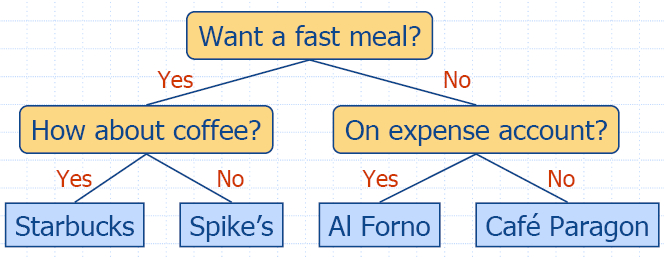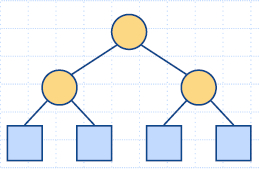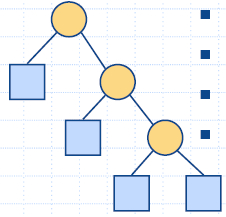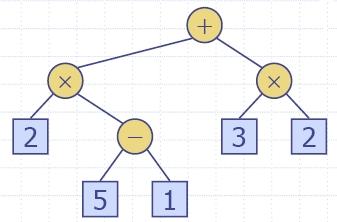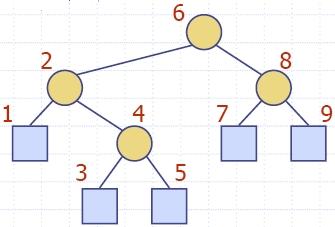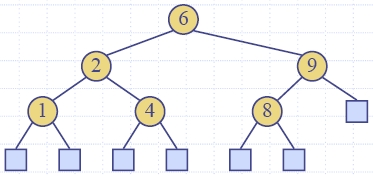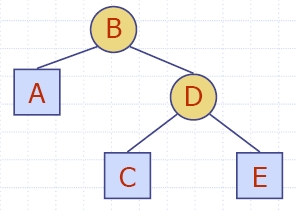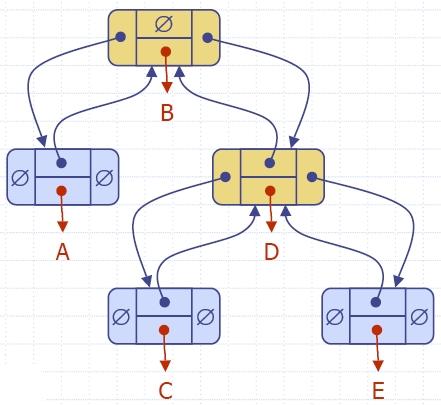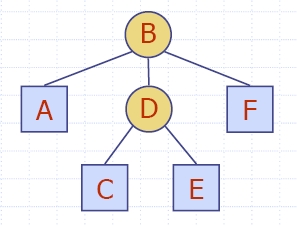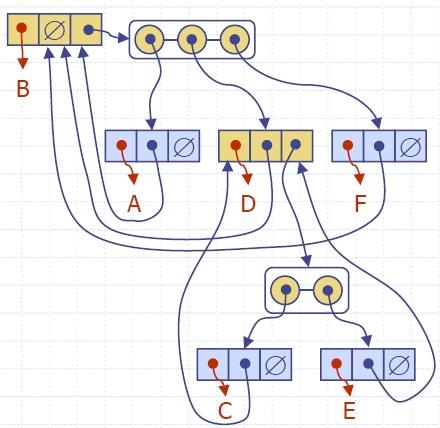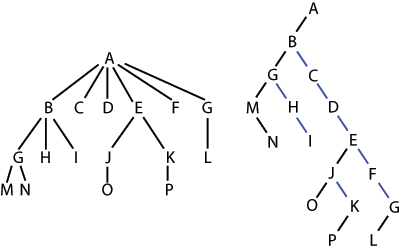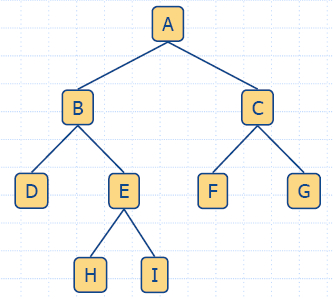
- Двоично дърво е дърво със следните свойства:
- Всеки вътрешен възел има две деца.
- Децата на възел са наредена двойка.
- Ще наричаме децата на вътрешен възел ляво дете и дясно дете.
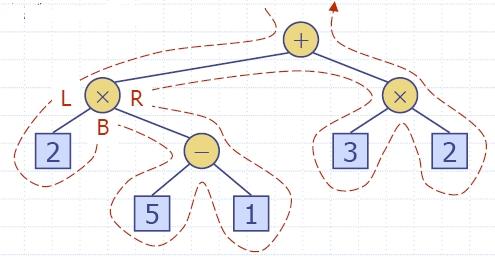
- Алтернативна рекурсивна (рекурентна) дефиниция: двоично дърво е или
- дърво, състояща се от един възел (корен) или
- дърво, чийто корен има наредена двойка наследници (ляво и дясно поддърво), всеки от които е двоично дърво.