6. Дървета - първа част

Дърво - дефиниция, терминология и основни свойства
Наредени дървета
Функции за дърво АТД
Дълбочина и височина на възел
Preorder обхождане
Postorder обхождане
Други видове обхождания

Дърво

• В компютърните науки дървото е абстрактен модел на йерархична структура.
• Дървото се състои от възли с връзки (релации) родител-дете.
• Приложения:
• диаграми;
• файлови системи;
• програмни среди.
• [Picture]
  

• Дървото T е съвкупност от възли за съхранение на елементи с връзката родител-дете със следните свойства:
  • T има специален възел r, наречен корен на T, който няма родител.
  • Всеки възел v на T, различен от r има единствен родител (parent node) u.
• Ако възел u е родител на възел v, казваме, че v е дете (наследник)  на u.
• Ако два възела са деца на един и същи родител, то те са братя (или сестри, siblings).
  
• Един възел е външен, ако няма деца и вътрешен, ако не е външен, т.е. има едно или повече деца. Външните възли се наричат листа.
• Поддърво на  T с корен възел v е дървото, състоящо се от всички наследници на v в T (включително v).
• Предшественик на един възел е или родителя му или предшественик на родителя му.
• Възел v е наследник на възел u ако u е предшественик на v.
• Пример:

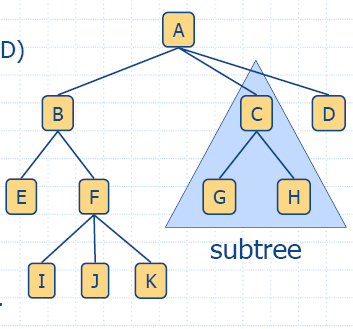
Корен: възел без родител (A) Вътрешен възел: възел с поне едно дете (A, B, C, F) Външен възел (т.е. лист ): връх без деца (E, I, J, K, G, H, D) Предшественик на възел (K): родител (F), баба (B), прабаба (A) Дълбочина на възел (F): брой на предшествениците (2) Височина на дърво: максимална дълбочина (3) на възел (J) Наследници на възел (A): дете (B), внуче (F), правнуче (I) Поддърво с корен (C) се състои от възел (C) и всички негови наследници (G, H) Линейно представяне: A(B(E, F(I, J, K)), C(G, H), D)

• Едно дърво е наредено, ако е дефинирана линейна наредба за децата на всеки възел (наредба на братя/сестри).
  
• Двоично дърво е наредено дърво в което всеки възел има най-много две деца.
• Едно двоично дърво е правилно, ако всеки възел има нула или две деца.
• За всеки вътрешен възел на двоично дърво означаваме децата му като ляво дете (ляв наследник) и дясно дете (десен наследник).
  
• Поддървото с корен лявото (дясното) дете на вътрешен възел v се нарича ляво поддърво (дясно поддърво) на v.

• Ще използваме позиции за абстракция на възлите:
• Object element(Position)       [link клас Positions]
  
• Общи методи (common methods):
• integer size()
• boolean isEmpty()
• ObjectIterator elements()      [link]
  
• PositionIterator positions()
• Методи за достъп (access methods):
• Position root()
• Position parent(Position)
• PositionIterator children(Position)
• Методи за запитване (query methods):
• boolean isInternal(Position)
• boolean isExternal(Position)
• boolean isRoot(Position)
• Методи за промяна (update methods):
• void swapElements(Position, Position)
• void replaceElement(Position, Object)
• Допълнителни методи за промяна могат да бъдат дефинирани в структурата от данни, която реализира дърво АТД.

• Tree.cpp

Основни операции за дърво АТД

• Ако v е външен възел, то неговата височина 0.
• Иначе, височината на v е 1 плюс максималната височина на децата му.

• 1. възел 2. наследници
• [Picture]
• За представеното графично дърво получаваме редицата: A B E F I J K C G H D

• 1. наследници 2. възел
• [Picture]
• За представеното графично дърво получаваме редицата: E I J K F B G H C D A

• Например бихме могли да обходим едно дърво, така че ще посетим всички възли с дълбочина d преди тези с дълбочина d+1 - обхождане в ширина - breadth-first search (BFS)
  
• [Picture]
• За представеното графично дърво получаваме редицата: A B C D E F G H I J K