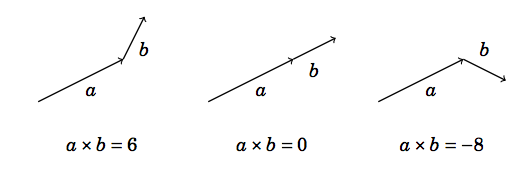7. Геометрични задачи [AL 29, p. 265]

План:
Задачи за домашно 7 и 8
Координатна система, точки и вектори
Отсечки и многоъгълници
Разстояния и лица
Изпъкнала обвивка
Задачи за домашно 9 и 10
** Координатна система, точки и вектори
- Точки и линии, a = (a1, a2), b = (b1, b2)

-- векторно произведение (cross product) axb = a1b2 - a2b1
cross
  дясна координатна система

-- положение на точка относно права
line
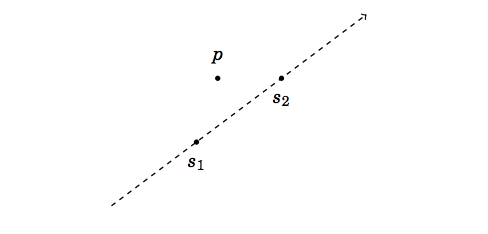
c = (p - s1) × (p - s2) показва местоположението на точката p относно правата, определена от точките s1 и s2. Ако c > 0, p се намира от лявата страна,  ако c < 0,  p е от дясната страна и ако c = 0,  точките s1,  s2 и p лежат на една права.

-- Скаларно произведение a.b = a1b1 - a2b2
перпендикуляни вектори a.b = 0
- Пресичане на отсечки (Line Segment Intersection)
-- Line–line intersection

- Многоъгълници (не самопресичащи се)
-- Точка в многоъгълник
inside

- Разстояние между две точки, дължина на вектор
Евклидово (l2) разстояние: e2 = (a1 - a2)2 + (b1 - b2)2
Манхатън (l1) разстояние: m = |a1 - a2| + |b1 - b2|
Чебишево (linf)разстояние: c = max{|a1 - a2|,  |b1 - b2|}

-- Ориентирано лице на многоъгълник (Shoelace Formula) [AL p. ]
polygonpick
A = |x1y2 + x2y3 + x3y4 + ... + xn-1yn + xny1 - x2y1 - x3y2 - ... - xnyn-1 - x1yn|/2

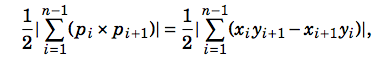
poly2

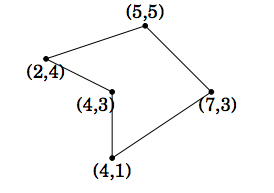
Пример: |(2·5−5·4)+(5·3−7·5)+(7·1−4·3)+(4·3−4·1)+(4·4−2·3)|/2 = 17/2
 (Polygon Area)

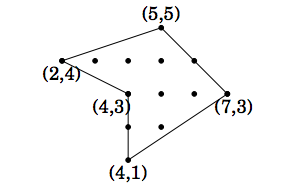
Теорема на Пик. Нека координатите на върховете на непресичащ се многоъгълник са цели числа. Тогава лицето на многоъгълника е S = a + b/2 - 1, където е a броят на целите точки вътре в многоъгълника и b е броят на целите точки на границата на многоъгълника.

Пример: 6 + 7/2 - 1 = 17/2
** Изпъкнала обвивка на множество от точки (Convex Hull) [AL р. 278]
Изпъкналата обвивка за дадено множество от точки P е изпъкнал многоъгълник с минимално лице, който съдържа изцяло множеството P.
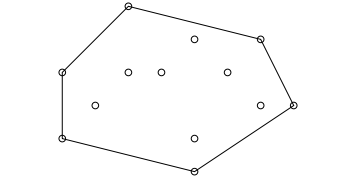
conv1conv2

Задача: Дадено е множество от точки в равнината. Да се намери затворената обвивка на множеството.
Алгоритъм на Андрю - O(n log n)
conv3
Телерик I, Телерик II

Други алгоритми

Най-близка двойка точки (Closest Points) [AL p. 277]

Х. Борисов, И. Тодоров, Геометрията в състезателното програмиране, I част, II част, 2009.

Три-ъгълници
https://www.hackerrank.com/fifth-interuniversity-nbu-programming-contest

Брой триъгълници
https://www.hackerrank.com/nbu-march-2020-programming-contest

Още геометрични задачи