13. Търсещи дървата - първа част

Речник АТД
Двоични дървета за търсене
- Търсене
- Операции за обновяване - вмъкване и изтриване
- Най-добър и най-лош случай
- C++ реализация
AVL дървета
- Вмъкване в AVL дърво
- Премахване на възел от AVL дърво
- Времена за изпълнение на операциите на речник АТД с реализация като AVL дърво
- C++ реализация

Речник АТД

• find(k) - Връща позицията на елемент с ключ k или nullposition, ако няма такъв ключ.
• findAll(k) - Връща позиционен итератор за всички обекти с ключ k.
• insertItem(k,e) - Вмъква обект (двойка) с елемент e и ключ k.
• removeElement(k) - Изтрива обект с ключ k. Възниква грешка, ако няма такъв елемент.
• removeAllElements(k) - Изтрива всички обекти, чийто ключ е равен на k.
• closestBefore(k)- Връща позиция на обект с най-голям ключ, по-малък или равен на k.
• closestAfter(k) - Връща позиция на обект с най-малък ключ, по-голям или равен на k.

Двоични дървета за търсене

• Двоично дърво за търсене е двоично дърво за съхранение на ключове (или двойки ключ-елемент) в своите вътрешни възли, които имат следното свойства:
• Нека u, v и w са върхове на дървото такива, че  u е в лявото поддърво на v и w е в дясното поддърво на v.
  Тогава key(u) ≤ key(v) ≤ key(w);
• Външните възли не съхраняват ключове.
• Inorder обхождане (ляво-корен-дясно) посещава ключовете на речника в ненамаляващ ред.

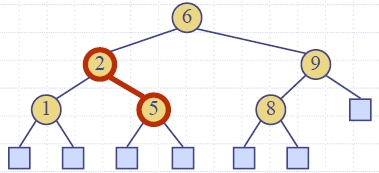
6(2(1, 4), 9(8, -)) Ключовете на речника в ненамаляващ ред: 1  2  4  6  8  9

• За търсене на ключ k, се върви по път надолу, тръгвайки от корена.
  
• Следващ възел за посещение (ляво или дясно дете) зависи от резултата от сравнението на k с ключа в текущия възел.
• Ако се достигне листо, ключът не е намерен и се връща nullposition.

• Примери: find(4), find(7)
  

Търсим 4: 4 < 6 - ляво 4 > 2 - дясно 4 = 4 - намерено! Търсим 7: 7 > 6 - дясно 7 < 9 - ляво 7 < 8 - ляво листо - няма!

• Функцията find(k) на речника D се изпълнява за време O(h), където h е височината на двоичното търсещо дърво T, използвано за реализацията на D.

Операции за обновяване (актуализиране)

• За да се изпълни операция insertItem(k, e), се търси с ключ k.
• Нека k не е в дървото и нека w е листото, достигнато при търсенето.
• k се поставя във възел w и w се разширява до вътрешен възел (операция expandExternal(w) на двоично дърво АТД).

• За да се изпълни операция removeElement(k), се търси с ключ k.
• Нека ключ k е в дървото и нека v е възелът, съхраняващ k.
• Ако възел v има дете листо w, изтриват се v и w от дървото  (операция removeAboveExternal(w) на двоично дърво АТД).

• Намира се вътрешен възел w, който следва v в inorder обхождане на дървото.
• Копира се key(w) във възела v.
• Изтрива се възел w и неговото ляво дете z (което е листо) с операция removeAboveExternal(z).

• Даден е речник с n членове, реализиран като двоично търсещо дърво с височина h.
• Използваната памет е O(n).
• Методите findElement(), insertItem() и removeElement() отнемат време O(h).
  
• Височината на дървото е O(n) в най-лошия случай и O(log n) в най-добрия случай.

Binary Search Trees, BST Sort - лекция в MIT

C++ реализация

AVL дървета

• Свойство височинен баланс (Height-Balance Property): За всеки вътрешен възел v от T разликата във височините на децата му може да бъде най-много 1.
• AVL дърво е двоично търсещо дърво със свойството височинен баланс.
  
• Adel'son-Vel'skii and Landis (Адельсон-Вельский, Ландис - 1968).
• Един възел в балансиран, ако разликата във височините на децата му е най-много 1.
  
• Твърдение: Височината на AVL дърво, съхраняващо n ключове е O(log n).

• Изпълнява се insertItem(k,e) - метод от базовия клас BST, вика се expandExternal(w) от двоично дърво АТД.
• Височината на дървото може да се увеличи и да се наруши свойството "височинен баланс".
• Ако има небалансиран възел:
  
  • Нека z е първият небалансиран възел, който срещаме по пътя от w към корена на T.
  • Нека y означава детето на z с по-голяма височина.
  • Нека x е детето на y с по-голяма височина.

• restructure(x)
  
• Нека a, b, c са x, y, z в редицата при inorder обхождане.
  
• Извършваме ротация на трите възела така, че b да е най-горе в дървото, т.е. b(a, c).
• Пример: insertItem(54, e)
  

• Има 4 възможни начина за изобразяване на  (x, y, z) в (a, b, c).

• Пример: insertItem(54, e)
  

• Тъй като това преструктуриране може да нарушава баланса на друг възел по-високо в дървото, трябва да продължим проверката за баланс до достигане на корена на T.
  

• Изпълнява се removeElement(k) - метод от базовия клас BST, вика се removeAboveExternal(w) от двоично дърво АТД.
  
• Премахването в двоичното търсещо дърво означава, че премахнатият възел става (празен) външен възел.
• Неговият родител w може да стане небалансиран възел.
• Пример: removeElement(32)

• restructure(x), както при вмъкване
  
  • Нека z е първият небалансиран възел w по пътя от w към корена на дървото.
  • Нека y е детето на z с по-голяма височина.
  • Нека x е детето на y с по-голяма височина.
• Изпълняваме операция restructure(x) за да възстановим баланса на z.
• Тъй като това преструктуриране може да нарушава баланса на друг възел по-високо в дървото, трябва да продължим проверката за баланс до достигане на корена на T.
  

• Една реконструкция отнема време O(1)
• като използваме реализация на двоично дърво със свързана структура
• find е O(log n)
• височината на дървото е O(log n), няма реконструкции
• insert е O(log n)
• началното търсене е O(log n)
• преструктуриране нагоре по дървото - не повече от O(log n)
• remove е O(log n)
• началното търсене е O(log n)
• преструктуриране нагоре по дървото - не повече от O(log n)

AVL tree - визуализация

AVL Trees, AVL Sort - лекция в MIT

C++ реализация