7. Дървета - втора част
Дефиниция и приложения
Двоично дърво АТД
Свойства на двоичните дървета
Обхождане на двоично дърво:
- Preorder обхождане
- Postorder обхождане
- Изчисляване на аритметичен израз
- Inorder обхождане
- Двоични дървета за търсене
- Ойлерово обхождане
Структури от данни за представяне на дървета
- Вектор-базирана структура
- Свързана структура
-- Възли и позиции на двоично дърво
-- Функции за обновяване на двоично дърво
-- С++ реализация на свързана структура на двиочно дърво
Представяне на дърво с двоично дърво
Двоични дървета
Двоично дърво е наредено дърво, в
което всеки възел има най-много две деца (преки
наследници).
Двоичното дърво е правилно, ако всеки вътрешен възел има точно
две деца.
 |
- Двоично дърво е дърво със следните свойства:
- Всеки вътрешен възел има две деца.
- Децата на възел са наредена двойка.
- Ще наричаме децата на вътрешен възел ляво дете и
дясно дете.
- Алтернативна рекурсивна (рекурентна) дефиниция:
двоично дърво е или
- дърво, състояща се от един възел или
- дърво, чийто корен има наредена двойка
наследници, всеки от които е двоично дърво.
|
Примери: аритметичен израз, дърво на решенията
Дърво за аритметичен израз

|
- Двоично дърво, свързано с аритметичен израз:
- вътрешни възли - операции;
- външни възли - операнди (аргументи).
- Пример: дърво за аритметичния израз
2 * (a −1) +
(3 * b)
|
Дърво
на решенията
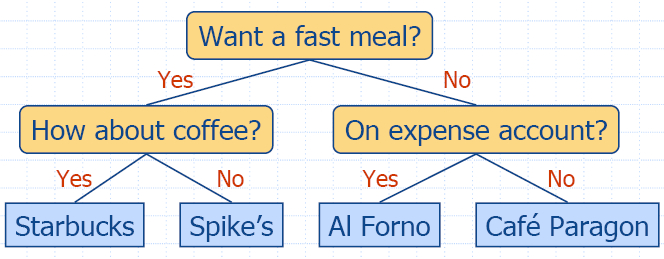 |
- Двоично дърво свързано с вземане на
решение:
- вътрешни възли - въпроси с отговор да/не;
- външни възли - решения.
- Пример: решение за хранене
|
Двоично дърво АТД
- Двоично дърво АТД (BinaryTree ADT) разширява
дърво AТД, т.е. то наследява всички методи на дърво АТД.
- Допълнителни методи:
- Position leftChild(p)
- Position rightChild(p)
- Position sibling(p)
- Методи за промяна на дървото се определят от структурата
за конкретната реализация на дърво АТД.
Интерфейс за двоично дърво
html-6.14a
(InspectableBinaryTree)
html-6.14b
(BinaryTree)
Свойства на двоичните
дървета
Множеството от всички възли на двоичното дърво T, които имат една и съща
дълбочина d, се нарича ниво
(level) d на T.
Нека T е правилно двоично дърво с
n възли и нека h е височината на T. Тогава T има следните свойства:
- Броят на външните възли e на T
е: h + 1 ≤ e ≤ 2h
- Броят на вътрешните възли i на T
е: h ≤ i ≤
2h − 1
- Общият брой на възлите n на T е: 2h + 1 ≤ n ≤
2h+1 − 1
- Височината h
на T е: log(n + 1) − 1 ≤ h ≤ (n − 1)/2
В правилното двоично
дърво T, броят на
външните възли e е с 1
повече от броя на вътрешните възли i, т.е. e
= i + 1.

 |
- Означения:
n - брой на
възлите;
e - брой на
външните възли;
i - брой на
вътрешните възли;
h - височина
на дървото.
- Свойства:
- e = i +
1
- n = 2e − 1
- h ≤ i
- h ≤ (n − 1)/2
- e ≤ 2h
- h ≥
log2e
- h ≥ log2(n + 1) − 1
|
Обхождане на двоично дърво
Preorder обхождане на двоично дърво
(корен, ляво поддърво, дясно поддърво - клд)
void binaryPreorderPrint(const Tree& T, const Position& v)
{ cout << v.element(); // print element
if (isInternal(v)) // visit children
{ cout << " ";
binaryPreorderPrint(T, T.leftChild(v));
binaryPreorderPrint(T, T.rightChild(v));
}
}
Postorder обхождане на двоично
дърво
(ляво поддърво, дясно поддъво, корен - лдк)
void binaryPostorderPrint(const Tree& T, const Position& v)
{ if (isInternal(v)) // visit children
{ cout << " ";
binaryPostorderPrint(T, T.leftChild(v));
binaryPostorderPrint(T, T.rightChild(v));
}
cout << v.element(); // print element
}
Изчисляване на
аритметичен израз

|
- Специализация на postorder обхождане:
- рекурсивен метод, връщаш стойността на
поддървото;
- при посещение на вътрешния възел се комбинират
стойностите на поддървета.
- Време за изпълнение O(n) (O(n)
time algorithm).
|
2 5 1 - x 3 2 x +
Обратен
полски запис
Пресмятане на аритметичен израз, записан като обратен полски
запис.
Стек: (2), (2,5), (2,5,1), (2,[5,1,-]), (2,4), ([2,4,x]), (8),
(8,3), (8,3,2), (8,[3,2,x]), (8,6), ([8,6,+]), (14)
Algorithm evalExpr(v)
if isExternal (v)
return
v.element ()
else
x
← evalExpr(leftChild (v))
y
← evalExpr(rightChild (v))
◊ ←
operator stored at
v
return x ◊ y |
Inorder
обхождане на двоично дърво
(ляво поддърво, корен, дясно поддърво - лкд)
 |
- При Inorder обхождане възелът се посещава след
лявото му поддърво и преди дясното му поддърво.
- Приложение: чертаене на двоично дърво
- x(v) = inorder ранг на v
- y(v) = дълбочина на v
- Посещения отляво-надясно.
|
Algorithm inOrder(v)
if isInternal (v)
inOrder(leftChild (v))
visit(v)
if isInternal (v)
inOrder(rightChild (v)) |
void binaryInorderPrint(const Tree& T, const Position& v)
{ if (isInternal(v)) // visit left child
binaryInorderPrint(T, T.leftChild(v));
cout << v.element(); // print element
if (isInternal(v)) // visit right child
binaryInorderPrint(T, T.rightChild(v));}
Двоични
дървета за търсене (търсещи двоични дървета)
Двоично дърво за търсене е двоично дърво, за което всеки
вътрешен възел v съдържа
елемент e, такъв, че:
- елементите от лявото поддърво на v са по-малки от
или равни на e и
- елементите от дясното поддърво на v са по-големи от
или равни на e.
 |
Търсим 4:
4 < 6 - ляво
4 > 2 - дясно
4 = 4 - намерено!
Търсим 7:
7 > 6 - дясно
7 < 9 - ляво
7 < 8 - ляво
листо - няма!
|
Position searchBinaryTree(const Tree& T, const Position& v, const Object& e)
{ if (isInternal(v))
if (v.element() == e) return v; // found!
else if (v.element() < e)
searchBinaryTree(T, T.leftChild(v), e); // search left subtree
else searchBinaryTree(T, T.rightChild(v), e); // search right subtree
else return ... // not found!
}
Времето t за търсене в двоичното дърво T е пропорционално на
височината на T, т.е. t >= O(log n) и t <= Omega(n).
Унифицирано
обхождане - ойлерово
обхождане на двоично дърво

|
- Обобщено обхождане на двоично дърво.
- Съдържа като специални случи preorder, postorder
и inorder обхождания.
- Разходка около дървото с посещение на всеки възел
три пъти::
- L - отляво (preorder)
- B - отдолу (inorder)
- R - отдясно (postorder)
|
+ x 2 2 2 x - 5 5 5 - 1 1 1 - x + x 3 3 3 x 2 2
2 x +
L L L B R B L L B R R L B R R R B L L B R B L B R R R
Структури от данни за представяне на дървета
Вектор-базирана структура за двоични дървета
Състои се от 4 успоредни вектори, например:
- obj съдържа обектите на контейнера;
- pred съдържа ранга на родителя;
- left съдържа ранга на лявото дете;
- right съдържа ранга на дясното дете.
rank: 0 1 2 3 4 5 6 7 8 9
obj: - A B C D E F G H I
pred: - - 1 1 2 2 3 3 5 5
left: - 2 4 6 - 8 - - - -
right: - 3 5 7 - 9 - - - -
Свързана структура за двоични дървета
- Възел е представен като обект, който съдържа:
- елемент;
- връзка към родител;
- връзка към ляв наследник;
- връзка към десен наследник.
- Обектите-възли са представени като позиции АТД.
Възли и позиции на двоично
дърво
html-6.27 (Node)
html-6.28
(Position)
Функции
за обновяване на двоично дърво
Добавяме още две функции:
- void expandExternal(const
Position& v)
- Position removeAboveExternal(const
Position& v)
С++ реализация на свързана структура на двиочно дърво
html-6.29
(LinkedBinaryTree1)
html-6.30
(LinkedBinaryTree2)
LinkedBinaryTree.cpp
Свързана
структура за дървета
- Възел е представен като обект, който съдържа:
- елемент;
- връзка към родител;
- редица от връзки към наследници.
- Възлите са представени като позиции АТД.
Представяне на дърво с
двоично дърво
Представянето на общо (наредено) дърво T се получава с
трансформация на T
в двоично дърво T '.
Трансформацията е следната:
- На всеки възел u
от T съответства
вътрешен възел u' от
T '.
- Ако u е външен
възел на T и няма
брат/сестра непосредствено след него/нея (в наредбата на
децата), то децата на u'
са външни възли на T '.
- Ако u е
вътрешен възел на T
и v е първо дете на
u в T, то v' e ляво дете на u' в T '.
- Ако възел v има
брат/сестра w
непосредствено след него/нея, тогава w' е дясно дете на v' в T '.
Пример:

Пример:
Допълнителни връзки:
http://www.cs.purdue.edu/homes/ayg/CS251/slides/chap5.pdf















