3. Представяне на граф. Обхождане на граф
План:
Задачи за домашно 1 и 2
Дефиниции
Представяне
Обхождане
Задачи за домашно 3 и 4
Дефиниции [5.1, стр. 247]
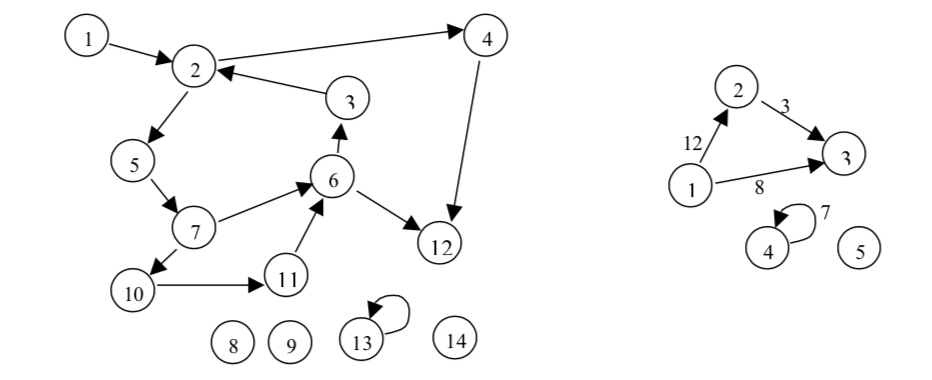
* Връх, възел (vertex, node), дъга, ребро (arc, edge), n
върха, m ребра
* Ориентиран и неориентиран граф
* Претеглен граф (дължини/тегла на дъгите)
* Предшественици и наследници, инцидентност (между връх и дъга),
съседност (върхове, дъги)
* Степен на връх се нарича броят на ребрата, инцидентни с него
* Път в граф
Пример: 10-11-6-3-2; 7, 6, 12
* Свързан граф, компоненти
на свързаност
Ориентиран граф се нарича слабо свързан, ако всеки два
върха i и j са краища на поне един път от i до j или от j до i).
Когато в ориентиран граф за всеки два върха i, j съществува път
както от i до j, така и от j до i, то графът се нарича силно
свързан.
Неориентиран граф се нарича свързан, ако съществува път между
всяка двойка негови върхове i, j.
* Цикъл
Пример: 5-7-6-3-2-5;
* Цикличен и ацикличен граф
* Мултиграф (повторение на ребра)
* Пълен граф - има дъга между всеки два върха
* Двуделен граф - две подмножества от върхове без дъги между
върховете във всяко от подмножествата
* Подграф - подмножество от върхове и всички дъги между тях
* Дърво (неориентиран
свързан граф без цикли), кореново дърво, покриващо дърво
Представяне [5.2]
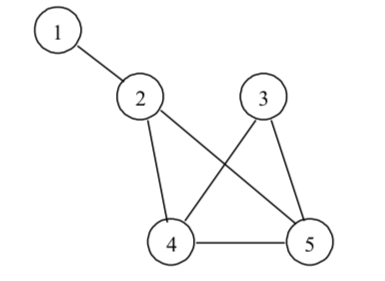
* Списък на ребрата [5.2.1]
Пример:
(1,2), (2,4), (2,5), (3,4), (3,5), (4,5)
памет O(m), съседни ребра O(m)
или O(log m)
* Матрица на съседство (достижимост) [5.2.2]
Пример:
1 2 3 4 5
1 0 1 0 0 0
2 1 0 0 1 1
3 0 0 0 1 1
4 0 1 1 0 1
5 0 1 1 1 0
памет O(n2), съществуване
на ребро между два върха O(1), наследници на връх O(n)
* Списък на наследниците [5.2.3]
Пример:
1 -> 2
2 -> 1, 4, 5
3 -> 4, 5
4 -> 2, 3, 5
5 -> 2, 3, 4
памет O(m), наследници на връх O(1), ребро
между два върха O(бр.насл.) или O(log бр.насл.)
* Матрица на инцидентност връх - дъга [5.2.4]
Пример:
1 2
3 4 5
(1,2) 1 1 0 0 0
(2,4) 0 1 0 1 0
(2,5) 0 1 0 0 1
(3,4) 0 0 1 1 0
(3,5) 0 0 1 0 1
(4,5) 0 0 0 1 1
памет O(m.n), ребро между
два върха O(m)
Обхождане [5.3]
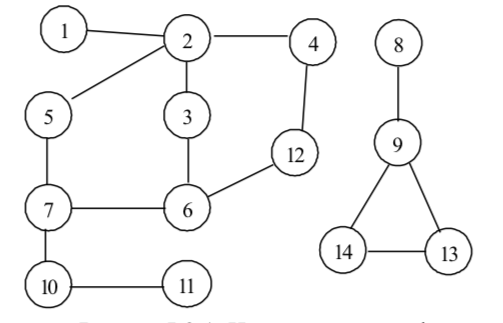
* Обхождане в ширина (BFS)
[5.3.1] лекция
в MIT
Пример:
1; (1)2; (2)3,(2)4,(2)5; (5)7,(3)6,(4)12;
(7)10; (10)11
* Обхождане в дълбочина (DFS)
[5.3.2]
Пример:
1,(1)2,(2)4,(4)12,(12)6,(6)7,(7)5;
(7)10,(10)11; (2)3
или
1,(1)2,(2)3,(3)6,(6)12, (12)4; (6)7, (7)10, (10)11;
(7)5
* Най-кратък път между два върха по брой на върховете [5.4.1]
Пример:
1, 2, 4, 12, 6 (път)
1 2, 3, 6 (най-кратък път)
* Проверка за цикличност [5.4.1]
* Намиране на всички прости пътища между два върха [5.4.1]
Пример:
1, 2, 4, 12, 6
1 2, 3, 6
1, 2, 5, 7, 6


