Nikolay Kirov
Research interests
Mesh generators and finite element solvers
Unstructured mesh generators and a finite element solver

Automatic unstructured mesh generation.

Triangle and tetrahedral meshing

Octree
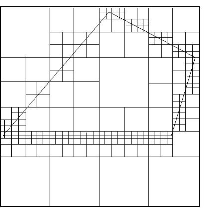
Cubes containing the geometric model are recursively subdivided until the desired resolution is reached. Irregular cells are then created where cubes intersect the surface. Tetrahedra are generated from both the irregular cells on the boundary and the internal regular cells.

Advancing front

The tetrahedra are built progressively inward from the triangulated surface. An active front is maintained where new tetrahedra are formed. As the algorithm progresses, the front will advance to fill the remainder of the area with triangles. Also required intersection checks to ensure that triangles do not overlap as opposing fronts advance toward each other.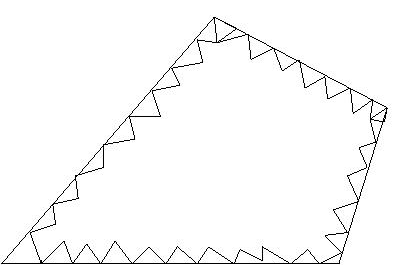

Delaunay
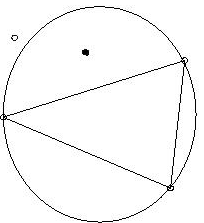
The Delaunay criteria: Any node must not be contained within the circumsphere of any tetrahedra within the mesh. Mesh the boundary of the geometry model to provide an initial set of nodes. The boundary nodes are then triangulated according to the Delaunay criterion. Nodes are then inserted incrementally into the existing mesh, redefining the triangles or tetrahedra locally as each new node is inserted to maintain the Delaunay criterion.

Methods:
- define nodes from a regular grid of points;
- nodes be recursively inserted at triangle or tetrahedral centroids;
- nodes at element circumcircle/circumsphere centers;
- advancing front approach to node insertion;
- point insertion along edges.
 

The mesh quality

The aspect ratio (a.r.) of the triangle or tetrahedron is the length of the longest edge divided by the length of the shortest altitude.

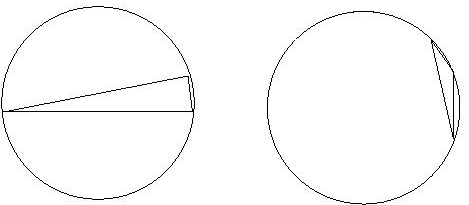
a.r. = 2/Ö3  » 1.15                                        a.r. =  4
 

The minimum angle a, gives a bound of p-2a of maximum angle and guarantees an aspect ratio between |1/sina| and |2/sina|.
 

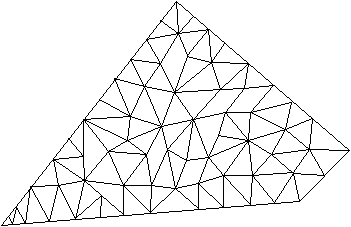
A skinny triangle will have a circumcircle much lager than its shortest edge. Tetrahedra can have roughly equal length edges, a reasonably sized circumsphere, and yet be arbitrary skinny.

Definition.
A tetrahedral shape measure is a continuous function that evaluates the quality of a tetrahedron. It must be invariant under translation, rotation, reflection and uniform scaling of the tetrahedron. It must be maximum for the regular tetrahedron and it must be minimum for a degenerate tetrahedron. There is no local maximum other than the global maximum for a regular tetrahedron and there is no local minimum other than the global minimum for a degenerate tetrahedron. For the easy of comparison, it should be scaled to the interval [0,1], and be 1 for the regular tetrahedron and 0 for a degenerate tetrahedron.

An aspect ratio function, defining by

g =
12
6
·
radius of inscribed sphere
length of largest edge
is a tetrahedral shape measure but minimum dihedral angle is not (according to the definition).
 

Mesh post-processing

Smoothing
Smoothing includes any method that adjust node locations while maintaining the element connectivity.
Methods:
 - Laplacian smoothing} - an internal nodes placed at the average location of any other node connected to it by an edge;
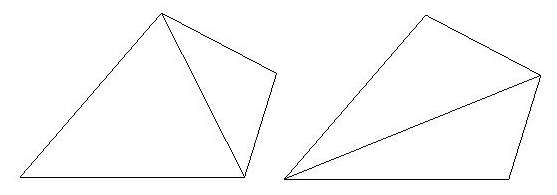
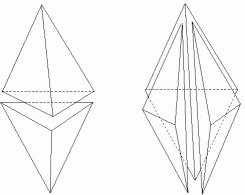
 - optimization-based smoothing techniques measure the quality of the surrounding elements to a node and attempt to optimize by computing the local gradient of the element quality with respect to the node location;
 - physically-based methods - reposition nodes using simulated physically based attraction or repulsion force.

Cleanup
Cleanup methods improve the quality of the mesh by making local changes to the element connectivities.
Topological improvement:

  • In 2D - simple diagonal swaps.

  • In 3D -- swapping two adjacent interior tetrahedra sharing the same face.

    •  

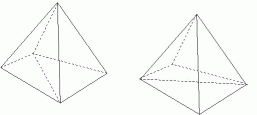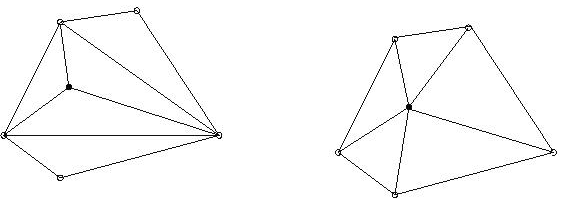
    Topological improvement -  attempt to optimize the number of edges sharing a single node (node degree).

    Refinement
    Refinement effectively reduces the local element size.

  •  Edge bisection involves splitting individual edges in the triangulation.
  •  Point insertion - to insert a single node at the centroid of an existing element, dividing the triangle into 3 or tetrahedron into 4.


    •  
  • Template - a specific decomposition of the triangle.

    • - decompose a triangle into 4 similar triangles by inserting a new node at each of its edges;
    - decompose tetrahedron into 8 tetrahedra where each face of the tetrahedron has been decomposed into 4 similar triangles.

         red refinement                                       green refinement
     

    Triangle

    [J. R. Shewchuk, Carnegie Mellon University]
    Triangle is a C-program for 2D mesh generation and construction of Delaunay triangulation and constrained Delaunay triangulation. \smallskip Main features:
  •  user-specified constraints on angles and triangle areas;
  • user-specified holes and concavities;
  • use of exact arithmetic to improve robustness.

    • Triangle's input is a planar straight line graph (PSLG) defined to be a collection of vertices and segments, where the endpoints of every segment are included in the list of vertices.

    # unite square
    4 2 0 1
    1 0.0 0.0 1
    2 0.0 1.0 1
    3 1.0 1.0 1
    4 1.0 0.0 1
    4 1
    1 1 2 1
    2 2 3 1
    3 3 4 1
    4 4 1 1
    0

    QMG

    [Stephan A. Vavasis, Cornell University]
    The Quality Mesh Generator (QMG) package does finite element mesh generation in two and three dimensions. The package includes geometric modeling software, the mesh generator itself and a simple finite element solver.  QMG consists of 60 MATLAB function and uses the scripting capabilities of MATLAB software package. The QMG handles complicated topology. The domain can have holes and quite complex internal boundaries. Input data have to be presented in form of a  brep. A  brep is a geometric object that is specified by its boundary faces. All breps must have flat boundaries, i.e. every element of the boundary must be a subset of a linear affine space. Abstractly, a brep is an acyclic directed graph. Every node in the graph stands for a face of the brep. The term "face'' refers to a vertex, edge or facet. The interior of the brep is also considered a face. Each of these faces has some information associated to it (for instance, vertices have their space coordinates associated with them). The arcs of the directed graph indicate boundary relationships. For example, an edge that is bounded by two vertices has arcs to those two vertices to indicate the bounding relation. A facet has arcs to the edges that act as its boundary.

    # unite cube
    < brep
     < 3 3
       < (
         < v0_0 (< point (0.0 0.0 0.0) >) () () >
         < v0_1 (< point (1.0 0.0 0.0) >) () () >
         < v0_2 (< point (0.0 1.0 0.0) >) () () >
         < v0_3 (< point (0.0 0.0 1.0) >) () () >
         < v0_4 (< point (1.0 1.0 0.0) >) () () >
         < v0_5 (< point (0.0 1.0 1.0) >) () () >
         < v0_6 (< point (1.0 0.0 1.0) >) () () >
         < v0_7 (< point (1.0 1.0 1.0) >) () () >
         )  < (
            < e1_0 () (v0_0 v0_1) () >
            < e1_1 () (v0_0 v0_2) () >
            < e1_2 () (v0_0 v0_3) () >
            < e1_3 () (v0_1 v0_4) () >
            < e1_4 () (v0_1 v0_6) () >
            < e1_5 () (v0_2 v0_4) () >
            < e1_6 () (v0_2 v0_5) () >
            < e1_7 () (v0_3 v0_5) () >
            < e1_8 () (v0_3 v0_6) () >
            < e1_9 () (v0_4 v0_7) () >
            < e1_10 () (v0_5 v0_7) () >
            < e1_11 () (v0_6 v0_7) () >
            )  < (
               < f2_0 () (e1_0 e1_1 e1_5 e1_3 ) () >
               < f2_1 () (e1_7 e1_10 e1_11 e1_8 ) () >
               < f2_2 () (e1_0 e1_4 e1_8 e1_2 ) () >
               < f2_3 () (e1_1 e1_2 e1_7 e1_6 ) () >
               < f2_4 () (e1_5 e1_9 e1_10 e1_6 ) () >
               < f2_5 () (e1_3 e1_4 e1_11 e1_9 ) () >
               ) < (
                 < d3_0 () (f2_0 f2_1 f2_2 f2_3 f2_4 f2_5) () >
               ) nil
             >
            >
           >
          >
         >
      >