l18

18. Още за рекурсията

Леймър, е програмист, който пише програми
в колонка и който, като чуе за рекурсия,
получава леко разстройство.
Преслав Наков, Панайот Добриков

Непряка рекурсия.
    Ако една функция f1 вика друга функция f2, а втората функция f2 вика първата f1, казваме, че има непряка рекурсия.
     Пример. Хилбертови криви.
    Хилбертова крива от 1-ви ред H₁ се получава като се чертае наляво - надолу - надясно единичната отсечка. H₂ се състои от 4 криви H₁ намалени наполовина, първата завъряна на +90, втората отместена на 1/2 наляво, третата отместена на 1/2 надясно и четвъртата завъртяна на -90 градуса и отместена 1/2 надясно. По същия начин е получена и кривата от 3-ти ред H₃ от H₂. Процесът може да продължи с получаване на H₄, H₅ и т. н. Има 4 елемента A, B, C и D, от които се състои всяка крива. За да напишем рекурсията, нека предположим, че можем да чертаем тези елементи и отсечки като "костенурка-графика":
- left - наляво;
- down - надолу;
- right - надясно;
- up - нагоре
с дължини 1/n за кривата H_n.


H₁	H₂	H₃

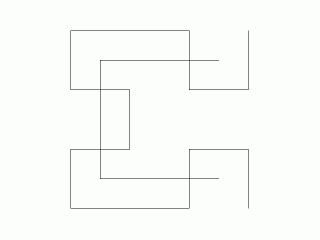
Получаваме следната схема на рекурсията:
A: left, down, right -> D left A down A right B
B: up,    right,down -> C up    B right B down A
C: right, up,   left -> B right C up    C left D
D: down, left, up    -> A down D left D up    C
Остава да се реализира "костенурка-графика", което може да се направи с познатата графична библиотека.
    Програма за чертаене на Хилбертови криви.
// hilbert.cpp
#include "ccc_win.cpp"

int h = 512; /* дължината на "единичната" отсечка */
int xold, yold; /* текущи координати на "костенурката" */
int x, y; /* нови координати на "костенурката" */

void Hilbert();
void A(int i);
void B(int i);
void C(int i);
void D(int i);

void plot()
/* ЦЕЛ: реализира "костенурка-графика" -
чертае отсечка, свързваща точките (xold, yold) и (x,y)в
*/
{ Line l(Point(x,y), Point(xold, yold));
cwin << l;
xold = x; yold = y;
}

void Hilbert()
{ int i = 0;
int x0 = h/2, y0 = h/2;
do
{ i++; h /= 2;
    x0 += h/2; y0 += h/2;
    xold = x = x0; yold = y = y0;
    A(i);
}
while (i < 5);
}

void A(int i)
{ if (i == 0) return;
D(i-1); x -= h; plot();
A(i-1); y -= h; plot();
A(i-1); x += h; plot();
B(i-1);
}
void B(int i)
{ if (i == 0) return;
C(i-1); y += h; plot();
B(i-1); x += h; plot();
B(i-1); y -= h; plot();
A(i-1);
}
void C(int i)
{ if (i == 0) return;
B(i-1); x += h; plot();
C(i-1); y += h; plot();
C(i-1); x -= h; plot();
D(i-1);
}
void D(int i)
{ if (i == 0) return;
A(i-1); y -= h; plot();
D(i-1); x -= h; plot();
D(i-1); y += h; plot();
C(i-1);
}

int main()
{ cwin.coord(0, h, h, 0);
Hilbert();
return 0;
}

Ефективност на рекурсията.
* Числа на Фибоначи.
Рекурсията е мощен инструмент за реализиране на ефективни алгоритми. В някои случаи обаче, тя може да доведе до лошо работещи алгоритми. Такъв е случаят с алгоритъма за пресмятане на числата на Фибоначи f_i, които се дефинират рекурентно така:

f₁= f₂= 1 и f_i= f_i_{- 1}+ f_i_{- 2} за i = 3, 4, ... . Рекурсивна функция за пресмятане на n-тото число на Фибоначи се пише лесно точно по рекурентната формула. Ще измерваме и времето за работа на тази функция.
// fibtime.cpp
#include <iostream>
using namespace std;
#include "ccc_time.cpp"

long fib(int n)
{ if (n <= 2) return 1;
else return fib(n - 1) + fib(n - 2);
}

int main()
{ cout << "Enter n: ";
int n;
cin >> n;
Time before;
long f = fib(n);
Time after;
cout << "fib(" << n << ") = " << f << "\n";
cout << "Elapsed time = " << after.seconds_from(before)
<< " seconds\n";
return 0;
}

Enter n: 30
fib(30) = 832040
Elapsed time = 2 seconds

Поставяме трасиращи печати във функцията, за да видим колко пъти се извиква функцията.
// fibtrace.cpp
#include <iostream>
using namespace std;

long fib(int n)
{ cout << "Entering fib: n = " << n << "\n";
long f;
if (n <= 2) f = 1;
else f = fib(n - 1) + fib(n - 2);
cout << "Exiting fib: n = " << n
<< " return value = " << f << "\n";
return f;
}

int main()
{ cout << "Enter n: ";
int n;
cin >> n;
long f = fib(n);
cout << "fib(" << n << ") = " << f << "\n";
return 0;
}

Enter n: 5
Entering fib: n = 5
Entering fib: n = 4
Entering fib: n = 3
Entering fib: n = 2
Exiting fib: n = 2 return value = 1
Entering fib: n = 1
Exiting fib: n = 1 return value = 1
Exiting fib: n = 3 return value = 2
Entering fib: n = 2
Exiting fib: n = 2 return value = 1
Exiting fib: n = 4 return value = 3
Entering fib: n = 3
Entering fib: n = 2
Exiting fib: n = 2 return value = 1
Entering fib: n = 1
Exiting fib: n = 1 return value = 1
Exiting fib: n = 3 return value = 2
Exiting fib: n = 5 return value = 5
fib(5) = 5

Този алгоритъмът за пресмятане на n-тото число на Фибоначи е неефективен, защото фунцията се извиква многократно с една и съща стойност на входния си параметър. За конкретния пример за да се пресметне fib(5)- fib(1) се вика 2 пъти, fib(2) - 3 пъти, fib(3) - 2 пъти и fib(4) - веднъж. Сложността на този алгоритъм е O(qⁿ), където q > 1.
Не е трудно да се реализира итеративен алгоритъм за решаване на същата задача.
// fibloop.cpp
#include <iostream>
using namespace std;
#include "ccc_time.cpp"

long fib(int n)
{ if (n <= 2) return 1;
long fold = 1;
long fold2 = 1;
long fnew;
for (int i = 3; i <= n; i++)
{ fnew = fold + fold2;
fold2 = fold;
fold = fnew;
}
return fnew;
}

Enter n: 45
fib(45) = 1134903170
Elapsed time = 0 seconds

В таблицата са дадени времената за работа на двата алгоритъма.

`n`	`fib(n)`	`rec sec`	`loop sec`
`30`	`832040`	`2`	`< 1`
`32`	`2178309`	`3`	`< 1`
`34`	`5702887`	`8`	`< 1`
`36`	`14930352`	`22`	`< 1`
`45`	`1134903170`	`-`	`< 1`

Нерекурсивният вариант за пресмятане на n-тото число на Фибоначи е по-ефективен.

* За пресмятане на n! и двата варианта - рекурсивния и итерационния - са еднакво ефективни.
* Двоичното търсене може да се направи нерекурсивно - двата варианта са приблизително еднакво ефективни..
* Сортиране чрез сливане е трудно да се направи нерекурсивно.
* Бързата сортировка може да си направи нерекурсивна.