14. Търсещи дървата - втора част
Многоканални търсещи дървета
-- Дефиниция
-- Търсене в многоканално търсещо дърво
(2,4) дървета
-- Дефиниция
-- Операции за промяна: вмъкване и премахване
Червено-черни дървета
-- Дефиниция
-- Операции за промяна: вмъкване и премахване
-- C++ реализация
Наредени дървета
Едно дърво е наредено, ако е дефинирана линейна наредба за децата на
всеки възел (наредба на братя/сестри).
Основни операции:
Position root();
Position parent(Position);
PositionIterator children(Position);
boolean isInternal(Position);
boolean isExternal(Position);
boolean isRoot(Position);
Многоканални търсещи дървета (Multi-Way Search Trees)
Дефиниция
- Възел v от
наредено дърво се нарича d-възел,
ако v има d деца.
- Многоканално търсещо дърво (multi-way search tree) е наредено дърво
такова, че:
- Всеки вътрешен възел v
има най-малко две деца (d-възел
с d >= 2);
- v съдържа d − 1 двойки
ключ-елемент (ki,
ei)
(d е броят на
децата), членове на речника;
- За възел с деца v1,
v2,
…, vd
съдържащ ключове k1
< k2 <
… < kd−1:
- ключовете в поддървото на v1 са по-малки от k1;
- ключовете в поддървото на vi са между ki−1
и ki (i = 2, …, d − 1);
- ключовете в поддървото на vd са по-големи от kd−1.
- Листата не съдържат ключове.
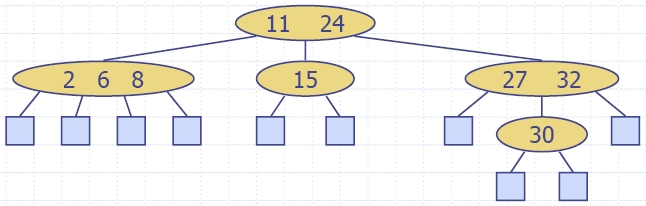
Пример: {11, 24}({2, 6, 8}, {15}, {27, 32}({30}))
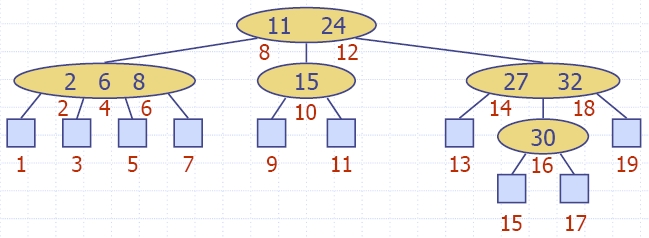
- Inorder обхождането за двоични дървета се разширява за
многоканални търсещи дървета с обхождане на ключовете във
всеки възел.
- Посещаваме двойката (ki,
ei) на
възела v между
рекурсивните обхождания на поддърветата на v с корени децата му vi и vi+1.
- Това (inorder) обхождане на многоканално търсещо дърво
нарежда ключовете в растящ ред.
Търсене
в многоканално търсещо дърво
Подобно е на търсене в двоични търсещи дървета.
- За всеки вътрешен възел с деца v1,
v2,
…, vd
и ключове k1,
k2,
…, kd−1 когато:
- k = ki (i = 1, …, d − 1): търсенето
завършва успешно;
- k < k1:
търсенето продължава с детето v1;
- ki−1
< k
< ki
(i = 2,
…, d − 1):
търсенето продължава с детето vi;
- k > kd−1:
търсенето продължава с детето vd.
- Достигането до външен възел завършва търсенето неуспешно.
- Пример:
search 30, search 20
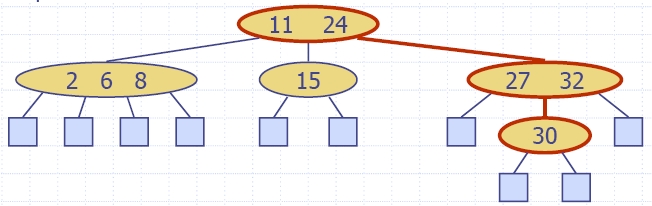
30 > 24 - дясно, 27 < 30 < 32 - долу,
30 = 30 - намерен ключ
11 < 20 < 24 - долу, 20 > 15 - дясно - листо, няма
такъв ключ
(2,4) дървета
Дефиниция
- (2,4) дърво (2-4
дърво или 2-3-4 дърво) е многоканално търсещо дърво със следните
свойства:
- Размер на възел
(Node-Size Property): всеки вътрешен възел
има най-много четири деца (и най-малко две).
- Дълбочина (Depth
Property): всички външни възли имат еднаква
дълбочина.
- В зависимост от броя на децата, вътрешен възел на (2,4)
дърво може да бъде 2-възел, 3-възел или 4-възел.
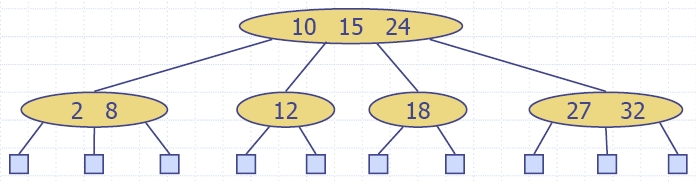
Пример: {10,15,24}({2,8}, {12}, {18},
{27,32})
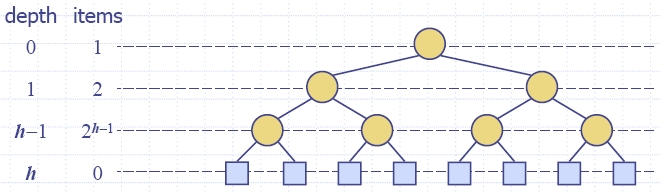
- Теорема:
(2,4) дърво с n
члена има височина O(log
n).
- Доказателство:
- Търсене в (2,4) дърво с n ключа отнема време O(log n).
Операции
за промяна (Update Operations)
Вмъкване
- Вмъкваме (добавяме) нов член (k, e)
към възела, който е родител
v на листoто,
достигнато при търсенето на ключ k.
- Свойството дълбочина се запазва.
- Може да възникне претоварване (overflow), т.е. възел v може да стане
5-възел.
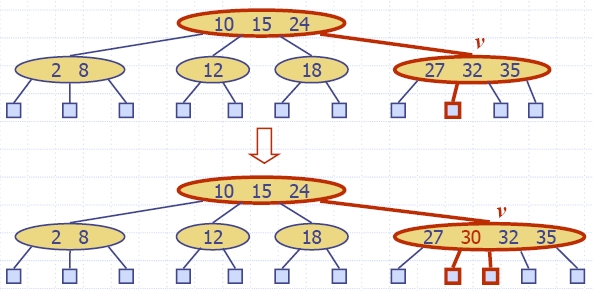
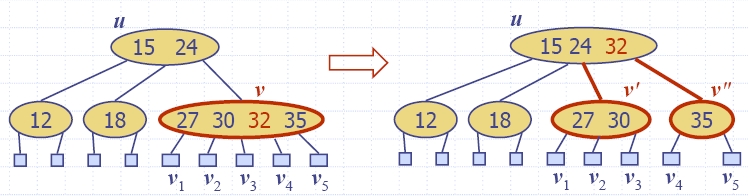
- Пример: вмъкване на ключ 30 предизвиква
претоварване
- Решение на претоварването е прилагане на операция разделяне (split):
- Нека v1,
…, v5 са децата на v и k1,
…, k4 са ключовете на v.
- Възел v
заместваме с възли v'
и v".
- v' е 3-възел
с ключове k1,
k2 и
деца v1,
v2,
v3.
- v" е 2-възел
с ключ k4
и деца v4,
v5.
- Ключ k3
се вмъква в родителя u
на v, като може да
възникне нов корен.
- Препълване може да се появи в родителския възел u,
за който трябва отново да се приложи операция разделяне.
- Препълването може да се разпространи до корена на
дървото.
Algorithm insertItem(k, e)
1.We search for
key k to locate the insertion node v
2.We add the new
item (k, e) at node v
3. while
overflow(v)
if isRoot(v)
create a new empty
root above v
v ← split(v)
|
Анализ
на вмъкването в (2,4) дърво
- Нека T е (2,4)
дърво с n ключа.
- Дървото T има
височина O(log
n).
- Търсенето е за време O(log
n), защото се
посещават O(log n) възли.
- Възстановяването на свойството "размер за възел" (Node-Size Property)
става за време O(log
n), защото всяка
операция разделяне (split)
отнема време O(1)
и се прилага не повече от O(log
n) пъти.
- Следователно вмъкването в (2,4) дърво става за време O(log n).
Премахване
(Removal)
- Нека ключът, който ще изтриваме е във възел с дете лист,
в противен случай заместваме ключа с неговия наследник (или
предшественик) при inorder обхождане на дървото (ключовете) и
след това го премахваме.
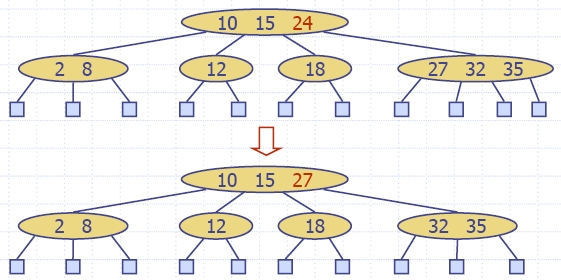
- Пример: за да изтрием ключ 24, го заместваме с 27
(inorder наследник)
- Изтриване на ключ от възела v може да доведе до изпразване (underflow), когато v става 1-възел с едно
дете и без ключове.
- За справяне с изпразването се разглеждат два случая:
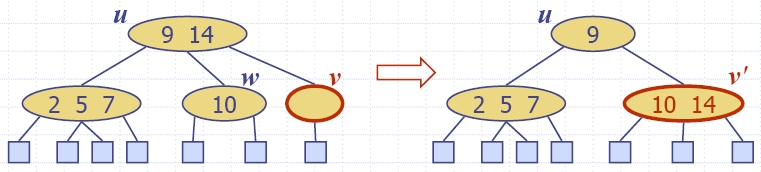
- Случай 1: съседен брат/сестра на v е 2-възел
- Операция
стопяване (fusion):
- слива се v със
съседния брат/сестра w;
- премества се ключ от u
в слетия възел v'.
Изпразването може да се появи по пътя към
корена и отново да трябва да се приложи операция
стопяване.
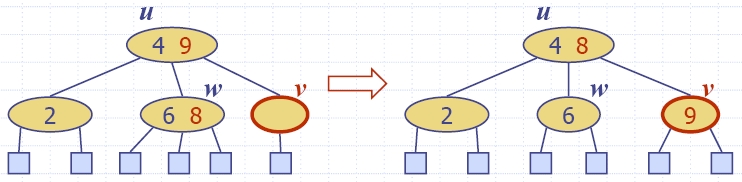
- Случай 2: съседния брат/сестра w на v
е 3-възел или 4-възел
- Операция
трансфер (transfer):
- премества се детето на w
и то става дете на v;
- премества се ключ от u
във v;
- премества се ключ от w
в u.
След тази операция няма изпразване.
Анализ
на операция премахване в (2,4) дърво
- Нека T е (2,4)
дърво (речник) с n
члена (ключа).
- Дървото T има
височина O(log n).
- За операция изтриване:
- Посетени са O(log
n) възли за да се
намери възела, от който ще бъде изтрит ключ.
- Препълване се обработва с редица от най-много O(log n) операции стопяване,
следвани от най-много една операция трансфер.
- Всяка една операция стопяване или трансфер отнема време
O(1).
- Следователно премахването на ключ от (2,4) дърво отнема
време O(log n).
B-Trees
- визуализация
Червено-черни дървета
Дефиниция
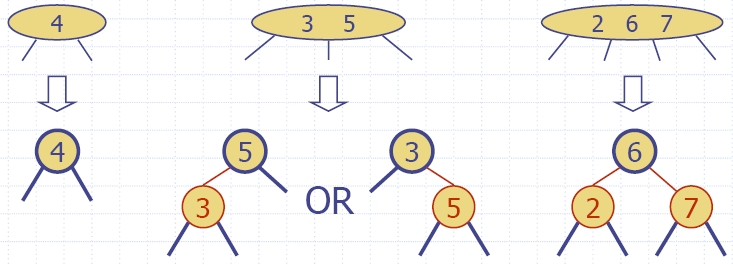
- Червено-черно дърво е
представяне на (2,4) дърво посредством двоично дърво, чийто
възли са оцветени червено или черно.
- В сравнение с неговото асоциирано (2,4) дърво, червено-черното дърво има:
- същото логаритмично време за изпълнение на основните
операции на речник АТД;
- по-лесно се реализира с еднотипни (с точност до цвят)
възли.
- Червено-черно дърво може да бъде
дефинирано като двоично дърво със следните свойства:
- Root Property:
коренът е черен;
- External Property:
листата са черни;
- Depth Property:
всички
листа имат еднаква черна дълбочина;
- Internal Property:
децата
на червен възел са черни.
Представяне на червено-черно
дърво: черните възли са bold, а червените - italic. Външните
възли не са включени в представянето.
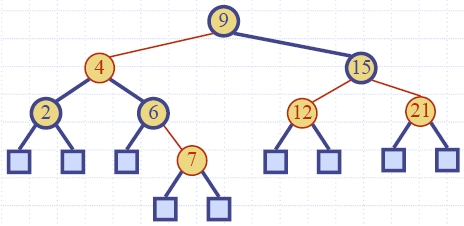
Пример: червено-черно
дърво: 9(4(2, 6(7)), 15(12,
21)) <-> (2, 4) дърво {4,
9}({2}, {6, 7}, {12, 15, 21})
- Теорема: Червено-черно дърво с n члена (ключа) има височина O(log n).
- Доказателство:
- Височината на червено-черно дърво е най-много два
пъти височината на (2,4) дърво, която е O(log n).
- Алгоритъмът за търсене в червено-черно дърво е същия,
както в двоично търсещо дърво и отнема време O(log n).
Операции
за обновяване
Вмъкване
- За да вмъкнем (добавим) член с операция insertItem(k, e), изпълняваме
алгоритъма "вмъкване" за двоично търсещо дърво и оцветяваме
новия възел z червен,
ако z не е корен.
- Така запазваме първите три свойства на червено-черно дърво.
- Ако родителят v
на z е черен,
то и последното свойство е изпълнено.
- Ако родителят v
на z е червен, имаме двойно
червено (т.е.
нарушаване на последното свойство), което изисква реорганизация на дървото.
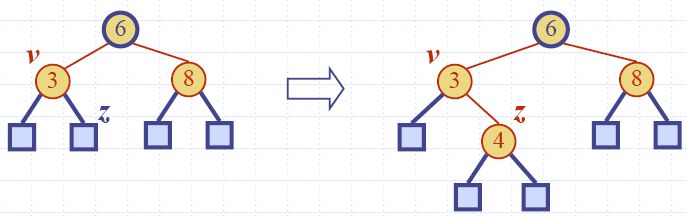
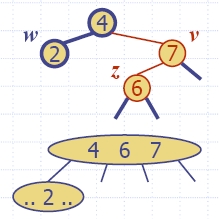
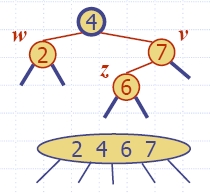
- Пример:
вмъкване на ключ 4 поражда двойно червено:
- Нека имаме двойно червено с дете z и родител v, и нека w е братът/сестрата на v:
|
- Случай 1: w
е черен:
- Двойнo червено е
неправилно представяне на 4-възел в (2,4) дърво.
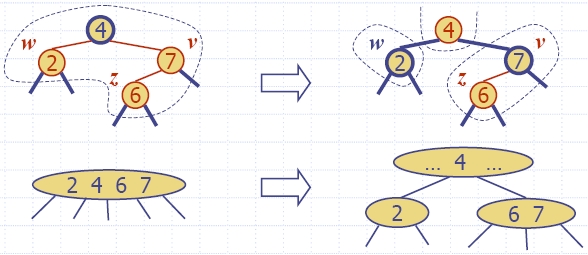
- С операция реконструкция
(restructuring) променяме представянето на
4-възел в (2,4) дърво.
|
|
- Случай 2: w
е червен:
- Двойно червено съответства на
препълване в (2,4) дърво.
- Операция преоцветяване
(recoloring) е еквивалентна на операция разделяне
(split) на 5-възел в (2,4) дърво.
|
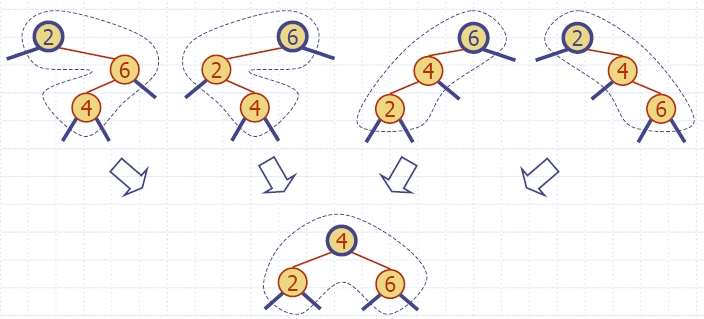
- Случай 1: Реконструкция (restructuring) на двойно червено,
когато червеният
родител v има черен брат/сестра
w.
- Има 4 конфигурации в зависимост от това дали двойното
червено е ляво или дясно (дясно-ляво, ляво-дясно,
ляво-ляво и дясно-дясно).
- Случай 2: Преоцветяване (recoloring) на двойно червено,
когато червеният
родител има червен брат/сестра.
- Родителят v и
неговият брат/сестра w
стават черни, възелът дядо/баба u става червен, освен ако не е
корен.
- Двойното
червено може
да разпространи по пътя към корена.
Анализ
на операция вмъкване в червено-черно дърво
- Височината на червено-черно дърво е O(log n).
- Търсенето отнема време O(log
n), защото са
посетени O(log n) възли.
- Вмъкване в двоично дърво отнема време O(1).
- Възстановяването на червено-черното
дърво отнема време O(log
n) защото:
- O(log n) преоцветявания,
всяко от които отнема време O(1) и
- най-много една реконструкция за време O(1).
- Следователно операция вмъкване в червено-черно дърво отнема време O(log n).
Премахване
(Removal)
- Първа стъпка на операцията remove(k)
е изпълнение на алгоритъма за изтриване в двоично дърво за
търсене.
- Нека v е
вътрешен възел за изтриване, w е дете на v за изтриване и r е брат/сестра на w.
- Ако v или r е червен, оцветяваме r в черно и сме
готови.
- Ако v и r са черни,
оцветяваме r в
черно и получаваме двойно черно, което
нарушава последното свойство и трябва да реорганизираме
дървото.
- Пример:
Изтриването на ключ 8 води до двойно черно.
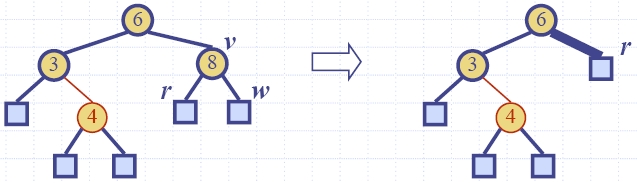
- Алгоритъмът за решаване на двойно черно за възел
r с брат/сестра y се разделя на 3 случая:
- Случай 1: y е черен и има червено дете
- Изпълняваме реконструкция (restructuring), еквивалентна на трансфер
(transfer), и сме готови.
- Случай 2: y е черен и неговите деца са черни.
- Изпълняваме преоцветяване (recoloring), еквивалентно на
стопяване (fusion)
в (2,4) дърво, след което двойно
черно може да се разпространи към корена на дървото.
- Случай 3: y е червен.
- Изпълняваме нагласяване (adjustment), еквивалентно на избор на
друго представяне на 3-възел, след което ще се появи Случай
1 или Случай 2.
- Изтриване в червено-черно дърво отнема време O(log n).
Реорганизация
на червено-черно дърво
Вмъкване (двойно червено)
Червено-черно дърво
|
(2,4) дърво
|
Резултат
|
| Реконструкция
(restructuring) |
Представяне на 4-възел
|
Двойно червеното изчезва
|
Преоцветяване
(recoloring)
|
Разделяне
(split)
|
Двойно червеното изчезва или се премества към
корена
|
Премахване (двойно черно)
Червено-черно
дърво
|
(2,4)
дърво
|
Резултат
|
Реконструкция
(restructuring)
|
Трансфер
(transfer)
|
Двойно черното изчезва
|
Преоцватяване
(recoloring)
|
Стопяване
(fusion)
|
Двойно черното изчезва или се премества към
корена |
Наместване
(adjustment)
|
Представяне на 3-възел
|
Следва реконструкция или преоцветяване
|
Red/Black Tree - визуализация
C++
Implementation
html-9.11 (RBItem)
html-9.12 (RBTree1)
html-9.13 (RBTree2)
html-9.14 (RBTree3)