Chapter 9

Chapter 9: Search Trees I

We study several alternative data structures based on trees for realizing ordered dictionary. The fundamental operations in an ordered dictionary ADT are:

find(k) - Return the position of an item with key k, and return a null position if no such item exists.
findAll(k) - Return an iterator of positions for all items with key k.
insertItem(k,e) - Inserts an item with element e and key k.
removeElement(k) - Remove an item with key k. An error condition occurs if there is no such item.
removeAllElements(k) - Remove all items with key equal to k.
closestBefore(k)- Return a position of an item with the largest key less than or equal to k.
closestAfter(k) - Return a position of an item with the smallest key greater than or equal to k.

9.1 Binary Search Trees (reminder)

A binary search tree is a binary tree storing keys (or key-element pairs) at its internal nodes and satisfying the following property:

Let u, v, and w be three nodes such that u is in the left subtree of v and w is in the right subtree of v.
We have key(u) ≤ key(v) ≤ key(w)
External nodes do not store items

Inorder traversal visits the keys of its dictionary in non-decreasing order.

9.1.1 Searching

To search for a key k, we trace a downward path starting at the root
The next node visited depends on the outcome of the comparison of k with the key of the current node
If we reach a leaf, the key is not found and we return a null position

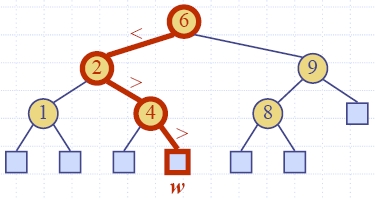
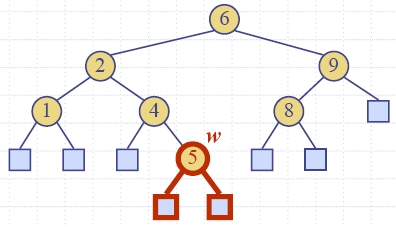
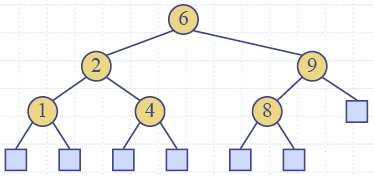
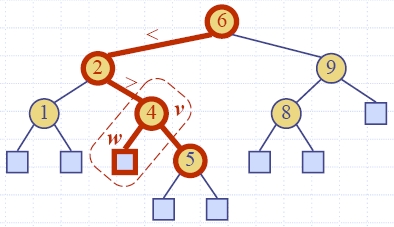
Algorithm find (k, v)
    if T.isExternal (v)
        return Position(null)
   if k < key(v)
        return find(k, T.leftChild(v))
   else if k = key(v)
        return Position(v)
   else { k > key(v) }
return find(k, T.rightChild(v))

Example: find(4)

Analysis of Binary Tree Searching

Function find(k) on dictionary D runs O(h) time, where h is the height of the binary search tree T used to implement D.

9.1.2 Update Operations

Insertion

To perform operation insertItem(k, e), we search for key k
Assume k is not already in the tree, and let w be the leaf reached by the search
We insert k at node w and expand w into an internal node (expandExternal(w))
Example: insert 5

Removal

To perform operation removeElement(k), we search for key k
Assume key k is in the tree, and let let v be the node storing k
If node v has a leaf child w, we remove v and w from the tree with operation removeAboveExternal(w)
Example: remove 4

We consider the case where the key k to be removed is stored at a node v whose children are both internal

we find the internal node w that follows v in an inorder traversal
we copy key(w) into node v
we remove node w and its left child z (which must be a leaf) by means of operation removeAboveExternal(z)

Example: remove 3

Best-case versus Worst-case

Consider a dictionary with n items implemented by means of a binary search tree of height h

the space used is O(n)
methods findElement(), insertItem() and removeElement() take O(h) time

The height is O(n) in the worst case and O(log n) in the best case

Binary Search Tree - visualization

Binary Search Tree - lecture

Binary Search Trees, BST Sort - lecture at MIT

9.1.3 C++ Implementation

A Binary Search Tree in C++
html-9.2 (Position)
html-9.3 (BST1)
html-9.4 (BST2)
html-9.5 (BST3)
html-9.6 (BST4)

except.h - LBTree.h - BSTree.cpp

9.2 AVL Trees

Height-Balance Property: For every internal node v of T the heights of the children of v can differ by at most 1.
An AVL Tree is a binary search tree with Height-Balance Property.
Adel'son-Vel'skii and Landis (Адельсон-Вельский, Ландис - 1968)
Proposition: The height of an AVL tree storing n keys is O(log n).

Insertion in an AVL Tree

insertItem(k,e) (expandExternal(w) in Binary tree ADT)
Let z be the first node we encounter in going up from w toward the root of T, such that z is unbalanced.
Let y denote the child of z with higher height.
Let x be the child of y with higher height.

Trinode Restructuring after an Insertion

restructure(x)
Let (a, b, c) be an inorder listing of x, y, z, perform the rotations needed to make b the topmost node of the three.

Example:

There are 4 possible ways of mapping (x, y, z) to (a,b,c).

Example:

Removal in an AVL Tree

removeElement(k)
Removal begins as in a binary search tree, which means the node removed will become an empty external node.
Its parent, w, may cause an imbalance.
Example:

Rebalancing after a Removal

Let z be the first unbalanced node encountered while traveling up the tree from w.
Also, let y be the child of z with the larger height.
Let x be the child of y with the larger height.
We perform restructure(x) to restore balance at z.
As this restructuring may upset the balance of another node higher in the tree, we must continue checking for balance until the root of T is reached.

Running Times for AVL Trees

a single restructure is O(1)

using a linked-structure binary tree

find is O(log n)

height of tree is O(log n), no restructures needed

insert is O(log n)

initial find is O(log n)
Restructuring up the tree, maintaining heights is O(log n).

remove is O(log n)

initial find is O(log n)
Restructuring up the tree, maintaining heights is O(log n).

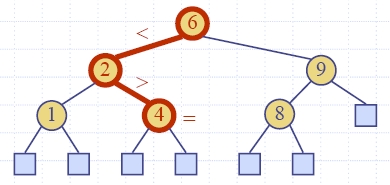
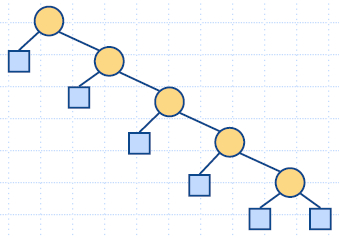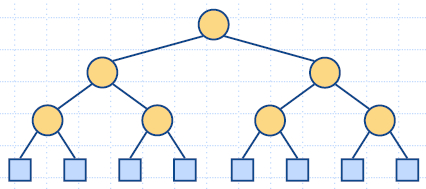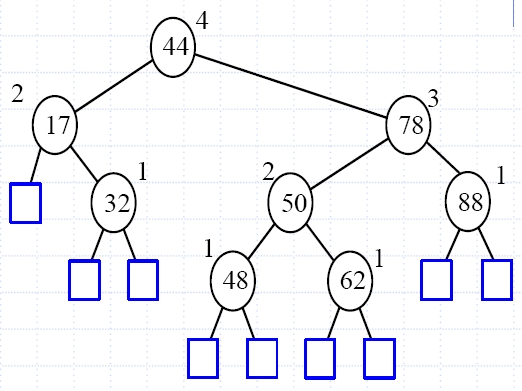
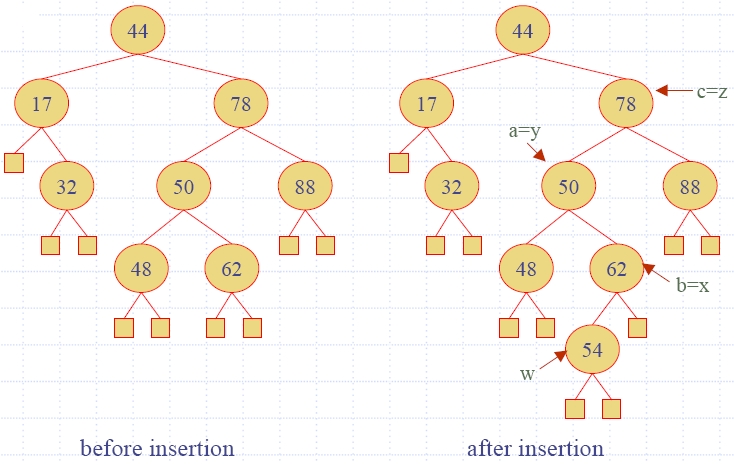
AVL tree - visualisation

AVL Trees, AVL Sort - lecture at MIT

9.2.2 C++ Implementation

html-9.8 (AVL Item)
html-9.9 (AVL Tree 2)
html-9.10 (AVL Tree 1)