12. Речници - втора част

Речник АТД
Хеш таблици
Клетъчни масиви (bucket arrays)
Хеш функции
Хеш кодове
Компресиращи изображения
Схеми за решаване на колизии
Реализация на хеш-таблица със C++

Речник АТД

• Речник АТД съхранява двойки ключ-елемент (k, e), които ще наричаме членове на речника (items), където k е ключ и e е елемент.
• Речник АТД използва позиции и поддържа следните функции за речника D:

Хеш таблици

• Един от най-ефективните начини за реализация на речник АТД е използването на хеш таблица.
• Въпреки, че хеш таблици имат голямо време за изпълнение за операциите на речник АТД в най-лошия случай (теоретична оценка), ще видим, че тяхното очаквано време за изпълнение в повечето случаи е отлично.
• Ако n означава броя на членовете на речника, времето за работа в най-лошия случай е O(n), но очакваното време за работа в общия случай е само O(1).

• Клетъчен масив за хеш таблица е масив A с размер N (капацитет), където всеки елемент на A се разглежда като клетка (т.е. контейнер за двойката ключ-елемент).
• Ако ключовете са цели положителни числа, добре разпределени в интервала [0, N - 1], този клетъчен масив е всичко, от което се нуждаем - двойката (k, e)  просто се поставя в клетка A[k].
• Ако ключовете не са уникални, тогава два елемента може да попаднат в една и съща клетка от A. В този случай казваме, че се появява колизия.

• Достижение: O(1) за всички функции, няма колизии за различни ключове.
• Недостатък 1: Използва памет О(N), твърде разточително когато N е голямо спрямо n.
• Недостатък 2: Ключовете са цели числа в интервала [0, N - 1], което често не е така.

Пример: Речник, състоящ се от (FN, name) - факултетен номер и име на студент, като речникът съхранява данни за студентите от този курс  (n < 100, N = 100000).

Хеш функции

• Хеш функция h изобразява ключове от даден тип  в цели числа от интервала [0, N − 1].
• Пример:
  h(x) = x mod N е хеш функция за цели числа (напр. FN mod 100)
  
• Цялото число h(x) се нарича хеш стойност на ключа x.
• Хеш таблица за даден тип ключове се състои от:
• хеш функция h,
  
• масив с размер N.
• Когато се реализира речник с хеш таблица, целта е да се постави обекта (k, e) в масива с индекс i =  h(k).
• Пример:

Да се направи хеш таблица за речник, съдържащ двойки (SSN, Name), където SSN (social security number) е 9-цифрово положително число. Ако хеш таблицата използва масив с размер N = 10000 и хеш функция h(x) = x mod 10000, т.е. (последните 4 цифри на x), може да възникнат колизии. За да се избегнат колизии, ще трябва да се вземе N = 109 и хеш функция h(x) = x (Недостатък 1).

• Хеш функцията h обикновено се разглежда като композиция на две функции:
  
• Хеш код: h₁: keys → integers
• Компресия: h₂: integers → [0, N − 1]
• Хеш кода се прилага първи и след това компресията се прилага върху резултата, т.е. h(x) = h₂(h₁(x)).
• Целта на хеш функцията е да "разпръсне" ключовете по (привидно) случаен начин.
• Хеш функцията е "добра", ако изобразява ключовете на речника така, че да минимизира колизиите.
• Тя трябва да бъде също така бърза и лесна за пресмятане.

Хеш кодове

• Цяло число, което съответства на ключа k се нарича хеш код или хеш стойност за k.

• Адреси на паметта:
  
• Преобразува се адреса (в паметта на компютъра) на ключа в цяло число - static_cast<int>(&key).
• Добър като цяло, с изключение на числови и низови ключове (има по-добри хеш кодове).
  
• Integer cast:
• Преобразуват се битовете на ключа в цяло число - static_cast<int>(key).
  
• Подходящ за ключове с дължина по-малка или равна на броя на битовете на числовия тип (например, char, short, int и float за много машини).
  
• Сума на компонентите:
• Разделят се битовете на ключа на компоненти с фиксирана дължина (например 16 или 32 бита) и се сумират компонентите (игнорирайки евентуално препълване).
• Подходящ за числови ключове с фиксирана дължина, по-голяма или равна на броя на битовете на числовия тип (например,  long и double за много машини).

int hashCode(int x)
{ return x; }

int hashCode(long x)
{  typedef unsigned long ulong;
   return hashCode(static_cast<int>(static_cast<ulong>(x) >> 32) 
          + static_cast<int>(x));
}

• Полиномиално натрупване:
• Разделят се битовете на ключа на редица от компоненти с фиксирана дължина (например, 8, 16 или 32 бита): a₀ a₁… a_n−1.
• Пресмята се стойността на полинома
  p(z) = a₀ + a₁z + a₂ z^₂ + … + a_n−1z^_n−1
  за фиксирана стойност на z, игнорирайки препълването.
• Особено подходящ за низове (напр. изборът z = 33 дава най-много 6 колизии за множество от 50000 английски думи!)
• Стойността на полиномът p(z) се смята за време O(n) по схемата на Хорнер:
• Следните полиноми се изчисляват последователно, като всеки от предишния, за време O(1) -
  p₀(z) = a_n−1,  p_i(z) = a_n−i−1 + zp_i−1(z) (i = 1, 2, …, n − 1).
• Получаваме p(z) = p_n−1(z).

int hashCode(const char* p, int len) // hash a character array
{ unsigned int h = 0;
  for (int i = 0; i < len; i++)
  { h = (h << 5)|(h >> 27);          // 5-bit cyclic shift
    h += (unsigned int)p[i];         // add in next character
  }
  return hashCode(int(h));
}

int hashCode(const double& x)       // hash a double
{ int len = sizeof(x);
  const char* p = reinterpret_cast<const char *>(&x);
  return hashCode(p, len);
}

Компресиращи изображения

• Хеш кода за ключ k обикновено не е подходящ за незабавнo използване с употреба с клетъчния масив, тъй като интервалът от възможни хеш кодове за ключовете обикновено надвишава интервала за допустими индекси на масива.

• h₂(y) = | y | mod N.
• Размерът N на хеш таблицата обикновено се избира просто число.
  
• Причината за това е свързана с теорията на числата и е извън обхвата на този курс.

• h₂(y) = |ay + b| mod N
• a и b са неотрицателни числа, такива че a mod N ≠ 0.
• В противен случай, всяко число ще се изобразява в една и съща стойност b.

Схеми за решаване на колизии

• Колизия възниква, когато различни елементи трябва да се поставят в една и съща клетка, т.е. ключовете им имат една и съща хеш стойност.

• Верижно съставяне: нека всяка клетка от таблицата е адрес на първия елемент на свързан списък.
• Верижно съставяне е просто, но изисква допълнителна памет извън таблицата.

Отворено адресиране

При колизия обектът се поставя в друга клетка на таблицата.

• Линейното пробване решава колизиите като поставя обекта в следващата свободна (кръгово) клетка на таблицата.
• Всяка проверена клетка на таблицата се разглежда като "проба".
• Недостатък/ Обектите с колизии се струпват, като следващите колизии предизвикват по-дълги редици от проби.
• Пример:
  

h(x) = x mod 13 Добавяме ключове 18, 41, 22, 44, 59, 32, 31, 73 в този ред: h(18) = 18 mod 13 = 5 --> a[5] = 18 h(41) = 41 mod 13 = 2 --> a[2] = 41 h(22) = 22 mod 13 = 9 --> a[9] = 22 h(44) = 44 mod 13 = 5 --> a[5] заета, a[6] = 44; h(59) = 59 mid 13 = 7 --> a[7] = 59 h(32) = 32  mod 13 = 6 --> a[6] заета, a[7]  заета, a[8] = 32 h(31) = 31 mod 13 = 5 --> a[5]-a[9] заети, a[10] = 31 h(73) = 73 mod 13 = 8 --> a[8]-a[10] заети, a[11] = 73

• За да се организират вмъквания и изтривания, се въвежда специален обект, наречен AVAILABLE (FREE), който замества изтритите обекти.
• removeElement(k)
• Търси се обект с ключ k.
• Ако обектът (k, e) е намерен, той се замества със специалния обект AVAILABLE и се връща позицията му.
• В противен случай се връща nullposition.
• insertItem(k, e)
• Ако таблицата е пълна, се изхвърля изключение.
• Започва се с клетка h(k).
• Пробват се последователно клетките докато се появи един от следните случаи:
• намерена е клетка i, която е празна или съдържа AVAILABLE, или
  
• N клетки са пробвани без резултат.
• В първия случай обектът (k, e) се поставя в клетка i.

• Двойно хеширане използва втора хеш функция d(k) и обработва колизии чрез поставяне на обекта в първата свободна клетка от серията (редицата):
  

             (h(k)+ jd(k)) mod N за j = 0, 1, … , N −1.

• Втората хеш функция d(k) не трябва да има нулеви стойности.
• Размерът N на таблицата трябва да бъде просто число, за да може да се пробват всички клетки.
• За компресията на втората хеш функция обикновено се избира функцията d₂(k) = q − k mod q, където
  
• q < N
  
• q е просто число.
  
• Възможни стойности на d₂(k) са 1, 2, … , q.
• Пример:

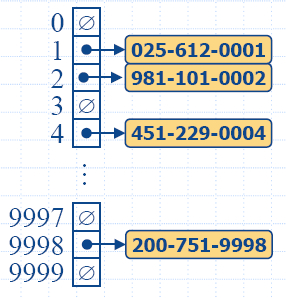
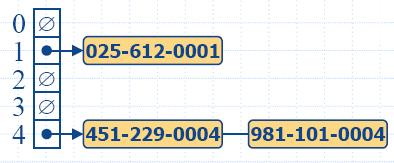
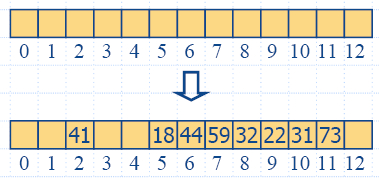
Разглеждаме хеш таблица за съхранение на целочислени ключове, обработваща колизии с двойно хеширане N = 13 h(k) = k mod 13 d(k) = 7 − k mod 7 Въвеждат се ключове 18, 41, 22, 44, 59, 32, 31, 73, в този ред: h(18) = 18 mod 13 = 5 --> a[5] = 18, (j = 0) h(41) =  41 mod 13 = 2 --> a[2] = 41, (j = 0) h(22) = 22 mod 13 = 9 --> a[9] = 22, (j = 0) h(44) = 44 mod 13 = 5 --> a[5] ,(j = 0), заета,         d(44) = 7 - 44 mod 7 = 7 - 2 = 5 -- > 5 + 1.5 = 10, a[10] = 44, (j = 1) h(59) = 59 mod 13 = 7 --> a[7] = 59, (j = 0) h(32) = 32  mod 13 = 6 --> a[6] = 32, (j = 0) h(31) = 31 mod 13 = 5 --> a[5] (j = 0), заетa,       d(31) = 7 - 31 mod 7 = 7 - 3 = 4 --> 5 + 1.4 = 9, a[9] (j = 1), заета,                          5 + 2.4 = 13, a[0] = 31, (j = 2); h(73) = 73 mod 13 = 8 --> a[8] = 73, (j = 0)