[]
[][]
[][][]
class Triangle {
public:
Triangle(int w);
int get_area() const;
private:
int width;
};
Triangle::Triangle(int w)
{ width = w; }
[]
int Triangle::get_area()
{ if (width == 1) return 1;
. . .
}
[]
[][]
[][][]
[][][][]
smaller_area + width
int Triangle::get_area()
{ if (width == 1) return 1;
Triangle smaller_triangle(width - 1);
int smaller_area = smaller_triangle.get_area();
return smaller_area + width;
}
#include <iostream> using namespace std
/** A class that describes triangle shapes like this: [] [][] [][][] . . . */
class Triangle { public: Triangle(int w); int get_area() const; private: int width;
}; /** Constructs a triangle with a given width. @param w the width of the triangle base */ Triangle::Triangle(int w) { width = w; } /** Computes the area of the triangle shape. @return the area */ int Triangle::get_area() const { if (width == 1) return 1; Triangle smaller_triangle(width - 1); int smaller_area = smaller_triangle.get_area(); return smaller_area + width; } int main() { Triangle t(4); cout << "Area: " << t.get_area() << endl; return 0; }
| nkirov@cpp % c++ triangle.cpp nkirov@cpp % ./a.out Area: 10 nkirov@cpp % |
double area = 0;
for (int i = 1; i <= width; i++) area = area + 1;
width * (width + 1) / 2
"eat"
"eta"
"aet"
"ate"
"tea"
"tae"
n! = 1 x 2 x 3 x . . . x n (x означава умножение)
n! = (n - 1)! x n
1! = 1
0! = 1
int factorial(int n)
{ if (n == 0) return 1;
int smaller_factorial = factorial(n - 1);
int result = smaller_factorial * n;
return result;
}
vector<string> generate_permutations(string word);
vector<string> v = generate_permutations("eat");
for(int i = 0; i < v.size(); i++)
cout << v[i] << "\n";
vector<string> generate_permutations(string word)
{ vector<string> result;
...
for (int i = 0; i < word.length(); i++)
{ string shorter_word = word.substr(0, i)
+ word.substr(i + 1, word.length() - i - 1);
...
}
return result;
}
vector<string> shorter_permutations
= generate_permutations(shorter_word);
for(int j = 0; j < shorter_permutations.size(); j++)
{ string longer_word = word[i] + shorter_permutations[j];
result.push_back(longer_word);
}
if (word.length() == 1)
{ result.push_back(word);
return result;
}
#include <iostream>
#include <string>
#include <vector>
using namespace std;
/**
Computes n!
@param n a nonnegative integer
@return n! = 1 * 2 * 3 * . . . * n
*/
int factorial(int n)
{ if (n == 0) return 1;
int smaller_factorial = factorial(n - 1);
int result = smaller_factoria * n;
return result;
}
/**
Generates all permutations of the characters in a string
@param word a string
@return a vector that is filled with all permutations
of the word
*/
vector<string> generate_permutations(string word)
{ vector<string> result;
if (word.length() == 1)
{ result.push_back(word);
return result;
}
for (int i = 0; i < word.length(); i++)
{ string shorter_word = word.substr(0, i)
+ word.substr(i + 1, word.length() - i - 1);
vector<string> shorter_permutations
= generate_permutations(shorter_word);
for (int j = 0; j < shorter_permutations.size(); j++)
{ string longer_word = word[i] + shorter_permutations[j];
result.push_back(longer_word);
}
}
return result;
}
int main()
{ cout << "Enter a string: ";
string input;
getline(cin, input);
cout << "There are " << factorial(input.length())
<< "permutations.\n";
vector<string> v = generate_permutations(input);
for (int i = 0; i < v.size(); i++)
cout << v[i] << endl;
return 0;
}
| nkirov@cpp % ./a.out Enter a string: eat There are 6 permutations. eat eta aet ate tea tae nkirov@cpp % |
recursive dancing
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, . . .
int fib(int n)
{ if (n <= 2) return 1;
else return fib(n - 1) + fib(n - 2);
}
| nkirov@cpp % ./a.out Enter n: 30 fib(30) = 832040 nkirov@cpp % ./a.out Enter n: 50 ^C nkirov@cpp % |
int fib(int n)
{ cout << "Entering fib: n = " << n << "\n";
int f;
if (n <= 2) f = 1;
else f = fib(n - 1) + fib(n - 2);
cout << "Exiting fib: n = " << n
<< " return value = " << f << "\n";
return f;
}
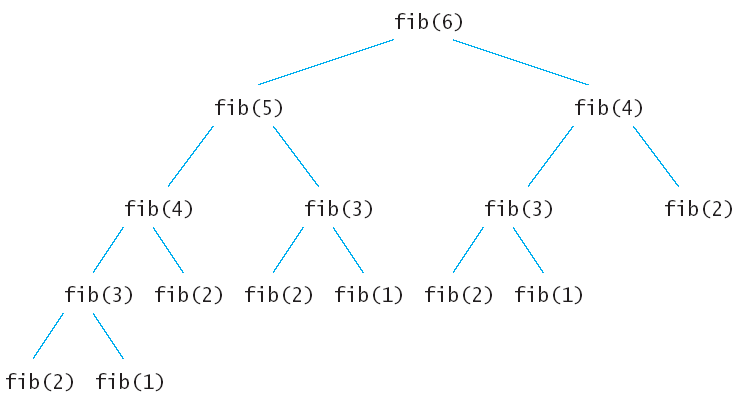
Entering fib: n = 6
Entering fib: n = 5
Entering fib: n = 4
Entering fib: n = 3
Entering fib: n = 2
Exiting fib: n = 2 return value = 1
Entering fib: n = 1
Exiting fib: n = 1 return value = 1
Exiting fib: n = 3 return value = 2
Entering fib: n = 2
Exiting fib: n = 2 return value = 1
Exiting fib: n = 4 return value = 3
Entering fib: n = 3
Entering fib: n = 2
Exiting fib: n = 2 return value = 1
Entering fib: n = 1
Exiting fib: n = 1 return value = 1
Exiting fib: n = 3 return value = 2
Exiting fib: n = 5 return value = 5
Entering fib: n = 4
Entering fib: n = 3
Entering fib: n = 2
Exiting fib: n = 2 return value = 1
Entering fib: n = 1
Exiting fib: n = 1 return value = 1
Exiting fib: n = 3 return value = 2
Entering fib: n = 2
Exiting fib: n = 2 return value = 1
Exiting fib: n = 4 return value = 3
Exiting fib: n = 6 return value = 8

int fib(int n)
{ if (n <= 2) return 1;
int fold = 1;
int fold2 = 1;
int fnew;
for (int i = 3; i <= n; i++)
{ fnew = fold + fold2;
fold2 = fold;
fold = fnew;
}
return fnew;
}
| nkirov@cpp % c++ fibloop.cpp nkirov@cpp % ./a.out Enter n: 30 fib(30) = 832040 nkirov@cpp % ./a.out Enter n: 50 fib(50) = -298632863 nkirov@cpp % |
3 + 4 * 5
(3 + 4) * 5
1 - (2 - (3 - (4 - 5)))
3 + 4 * 5
(3 + 4) * 5
// eval.cpp #include <iostream> using namespace std;
int term_value(); int factor_value(); /** Evaluates the next expression found in cin @return the value of the expression. */ int expression_value() { int result = term_value(); bool more = true; while (more) { char op = cin.peek(); if (op == '+' || op == '-') { cin.get(); int value = term_value(); if (op == '+') result = result + value; else result = result - value; } else more = false; } return result; } /** Evaluates the next term found in cin @return the value of the term. */ int term_value() { int result = factor_value(); bool more = true; while (more) { char op = cin.peek(); if (op == '*' || op == '/') { cin.get(); int value = factor_value(); if (op == '*') result = result * value; else result = result / value; } else more = false; } return result; } /** Evaluates the next factor found in cin @return the value of the factor. */ int factor_value() { int result = 0; char c = cin.peek(); if (c == '(')
{ cin.get(); result = expression_value(); cin.get(); // read ")" } else // assemble number value from digits { while (isdigit(c)) { result = 10 * result + c - '0'; cin.get(); c = cin.peek(); }
} return result; } int main() { cout << "Enter an expression: "; cout << expression_value() << endl; return 0; }
| nkirov@cpp % ./a.out Enter an expression: (3+4)*5 35 nkirov@cpp % |