do
{ statements
}
while (condition);
x0
= a, xn+1
= ( xn +
a/xn )
/ 2
converges and has a limit square
root of a.
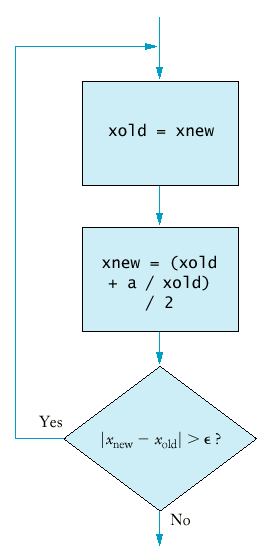
do
{ xold = xnew;
xnew = (xold + a / xold) / 2;
}
while (fabs(xnew - xold) > EPSILON);