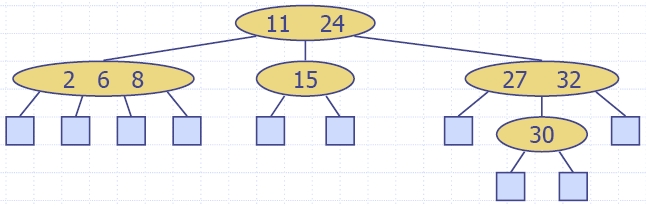

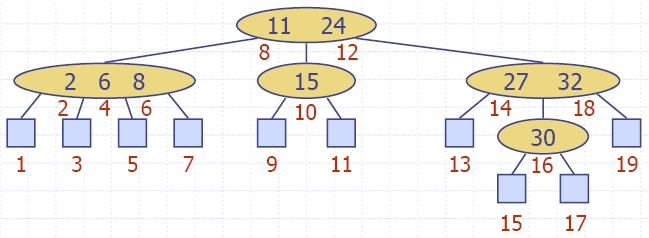
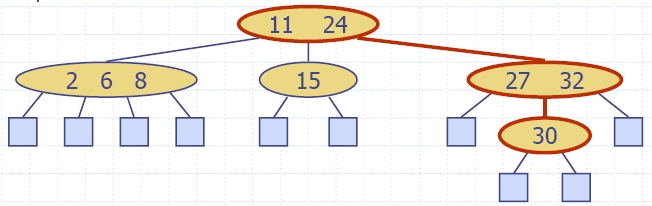
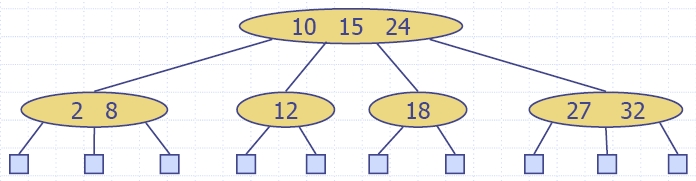
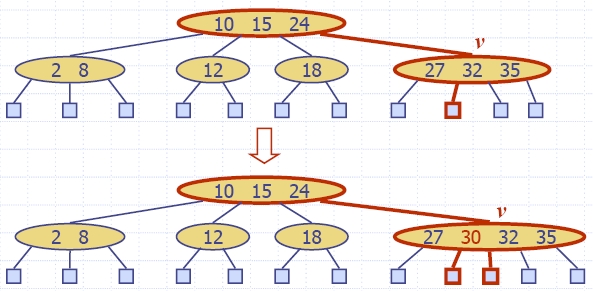
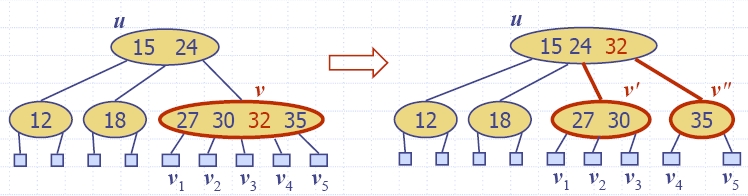
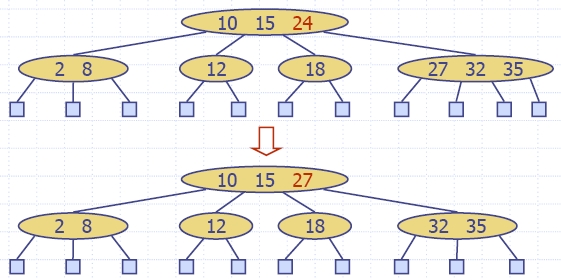
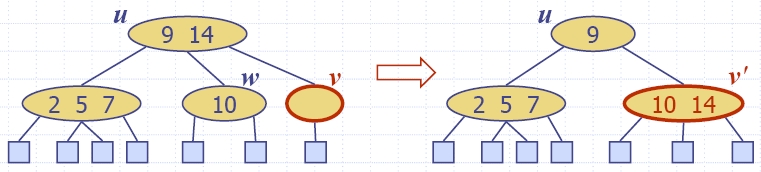
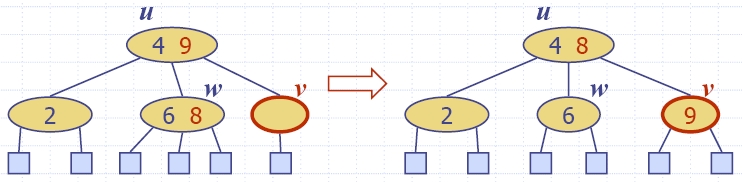
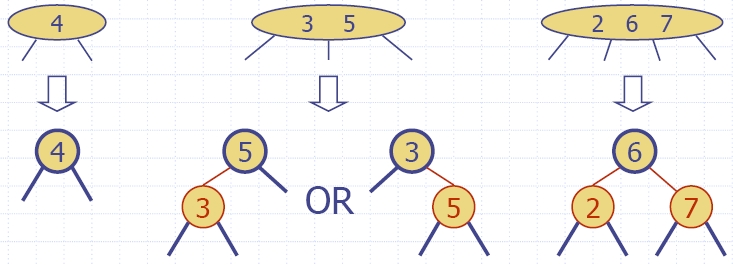
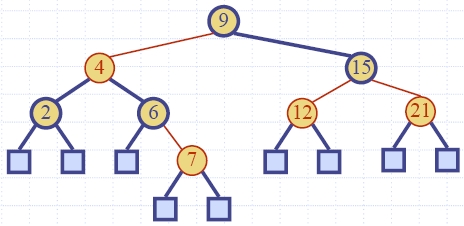
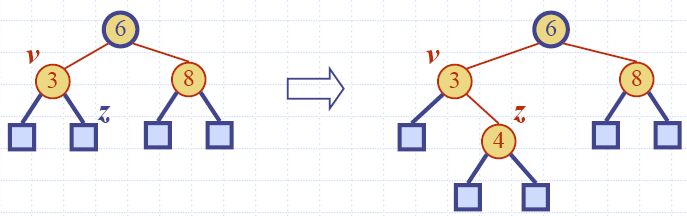
| Algorithm insertItem(k, e) 1.We search for key k to locate the insertion node v 2.We add the new item (k, e) at node v 3. while overflow(v) if isRoot(v) create a new empty root above v v ← split(v) |
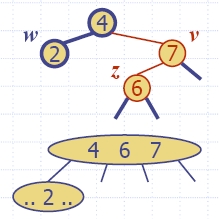 |
|
 |
|
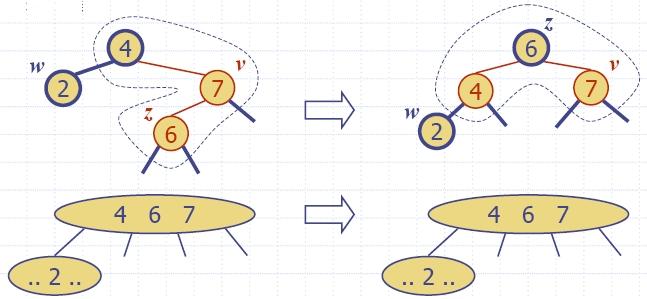
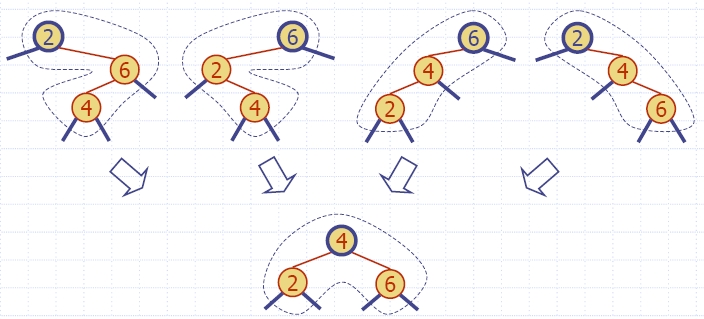
| Red-black tree action |
(2,4) tree action |
result |
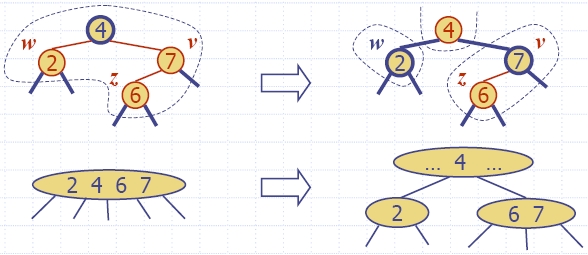
| restructuring | change of 4-node representation |
double red removed |
| recoloring |
split |
double red removed or propagated up |
| Red-black
tree
action |
(2,4) tree action | result |
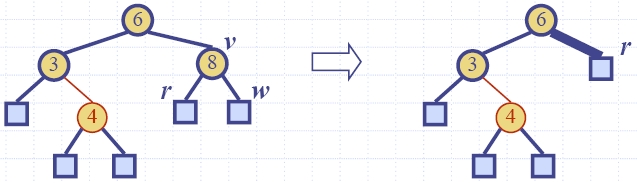
| restructuring |
transfer |
double black removed |
| recoloring |
fusion |
double black removed or propagated up |
| adjustment |
change of 3-node representation |
restructuring or recoloring follows |