l4

4. Редица на Фибоначи. Най-голям общ делител, най-малко общо кратно. Рекурсия

Редица на Фибоначи (Уикипедия) (Wikipedia) (YouTube)

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

F(0) = F(1) = 1
F(n+1) = F(n-1) + F(n) , n > 1

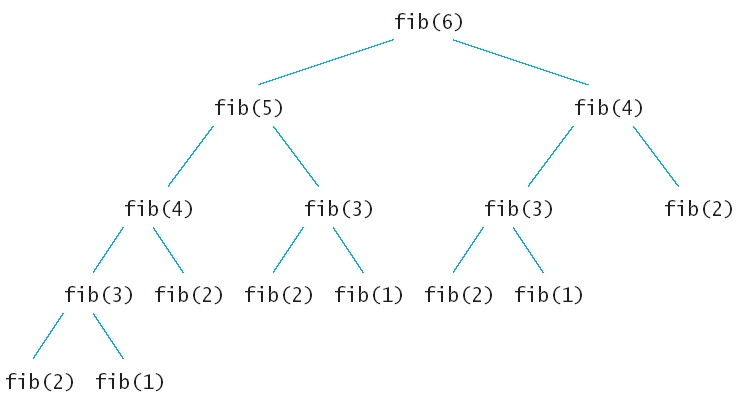
int fib(int n)
{ if (n <= 2) return 1;
else return fib(n - 1) + fib(n - 2);
}

int fib(int n)
{  cout << "Entering fib: n = " << n << "\n";
   
int f;
   if (n <= 2) f = 1;
   else f = fib(n - 1) + fib(n - 2);
   
cout << "Exiting fib: n = " << n
      << " return value = " << f << "\n";
   
return f;
}


int fib(int n)
{  if (n <= 2) return 1;
   int fold = 1;
   int fold2 = 1;
   int fnew;
   for (int i = 3; i <= n; i++)
   {  fnew = fold + fold2;
      fold2 = fold;
      fold = fnew;
   }
   return fnew;
}

** Най-голям общ делител [1.2.3]

* Алгоритъм на Евклид за намиране на най-голям общ делител

// gcd.cpp
#include <iostream>
using namespace std;

unsigned gcd1(unsigned a, unsigned b)
{ unsigned swap;
while (b > 0) { swap = b; b = a%b; a = swap; }
return a;
}

unsigned gcd2(unsigned a, unsigned b)
{ return (0 == b) ? a : gcd2(b, a%b); }

int main()
{ const unsigned a = 1, b = 125;
cout << gcd1(a, b) << endl;
cout << gcd2(a, b) << endl;
return 0;
}
* Да се напише метода само с изваждане.

** Връщане от рекурсия и използване на променливите [1.2.5]
* Рекурсивно отпечатване на цифрите на число

// digit2.cpp
#include <iostream>
using std::cout;

void printN(unsigned n)
{ if (n >= 10) printN(n/10);
cout << n%10;;
}
int main()
{ unsigned m = 1234;
printN(m);
return 0;
}

* Пресмятане на n! и изследване на ефективността на реализациите [1.2.5]

/* Два варианта за пресмятане на n! [1.2.5] */
// fact.cpp
#include <iostream>

unsigned long fact1(unsigned i)
{ if (1 == i) return 1;
return i * fact1(i - 1);
}

unsigned i;
unsigned long fact2()
{
    if (1 == i) return 1;
        return i-- * fact2(); // --i*fact();
}

const unsigned n = 6;
int main()
{
std::cout << "fact1: " << n << "! = " << fact1(n) << endl;
  i=n; // i=n+1;
std::cout << "fact2: " << n << "! = " << fact2(n) << endl;
return 0;
}

** Рекурсия и използване на глобални променливи [1.2.5]
* За дадено естествено число n (n < 9) да се отпечатат в нарастващ и намаляващ ред числата 10^k (0 < k < n).

// print0.cpp
#include <iostream>
using std::cout;
using std::cin;
using std::endl;

const unsigned n = 6;

void printRed1(unsigned k, unsigned long res)
{ cout << res << " ";
if (k < n) printRed1(k + 1, res*10);
cout << res << " ";
}

unsigned k = 0;
void printRed2(unsigned long res)
{ k++;
cout << res << " ";
if (k < n) printRed2(res*10);
cout << res << " ";
}

unsigned long res = 1;
void printRed3()
{  k++;
res *= 10;
  cout << res << " ";
if (k < n) printRed3();
  cout << res << " ";
res /= 10;
}

int main()
{
printRed1(1,10); cout << endl;
printRed2(10);   cout << endl;
k = 0;
printRed3();   cout << endl;
return 0;
}