Chapter 7: Priority Queues - II
7.3 Heaps
-
An efficient realization of a priority queue uses a
(nonlinear)
data structure called a heap − performs both
insertions and removals in logarithmic
time O(log n).
7.3.1 The Heap Data
Structure
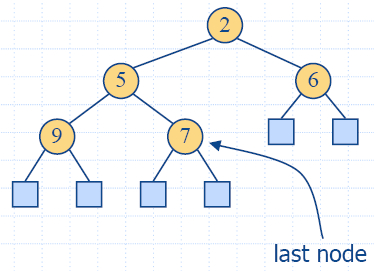
- A heap is a binary tree storing keys at its internal nodes
and satisfying the following properties:
- Heap-Order: for
every internal node v other
than the root, key(v) ≥ key(parent(v))
- Complete Binary Tree:
let
h be the height of the
heap
- for i = 0, … ,
h − 2, there are 2i nodes of depth i
- at depth h −
1,
the internal nodes are to the left of the
external nodes
- The last node of a
heap is the rightmost internal node of
depth h − 1
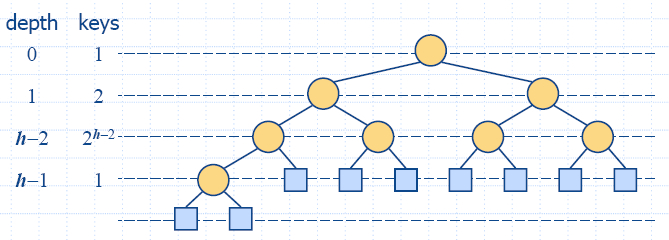
Proposition 7.5: A heap T
storing n keys has height h = [log(n + 1)].
Proof: (we apply the complete binary tree property)
- Let h be the
height of a heap storing n
keys
-
Since there are 2i
keys at depth i = 0, … , h −2 and at least one key at
depth h −1, we have n ≥ 1 + 2 + 4 +… + 2h −2 + 1 = 2h −1, thus, n ≥ 2h − 1, i.e. h ≤ log n + 1
-
Since for complete binary tree when there are 2h − 1 keys
at depth h −1,
we
have
n ≤
1 + 2 + 4 +… + 2h −1
= 2h −1,
thus, n ≤
2h −1,
i.e.
h ≤ log (n + 1)
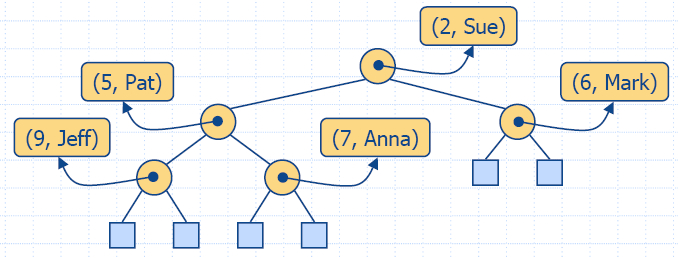
7.3.2 Implementing a
Priority Queue with a Heap
- We can use a heap to implement a priority queue
- We store a (key,
element) item at each
internal node
- We keep track of the position of the last node
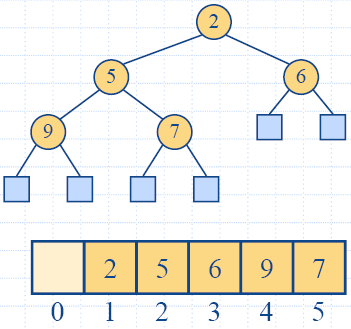
The Vector Representation
of a Heap
- We can represent a heap with n keys by means of a vector of
length n + 1
- For the node at rank i
- the left child is at rank 2i
- the right child is at rank 2i +1
- Links between nodes are not explicitly stored
- The leaves are not represented
- The cell of at rank 0 is not used
- Operation insertItem
corresponds to inserting at rank n
+ 1
- Operation removeMin
corresponds to removing at rank 1
- Yields in-place heap-sort
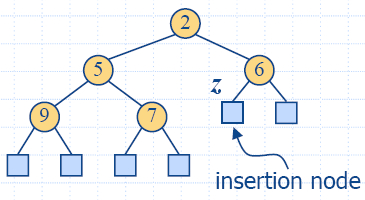
Insertion
- Method insertItem
of the priority queue ADT corresponds to
the insertion of a key k to
the heap
- The insertion algorithm consists of three steps
- Find the insertion node z
(the new last node)
- Store k at z and expand z into an internal node
- Restore the heap-order property (discussed next)
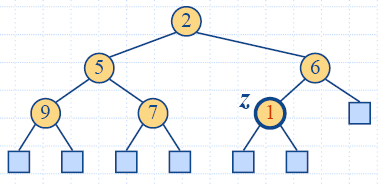
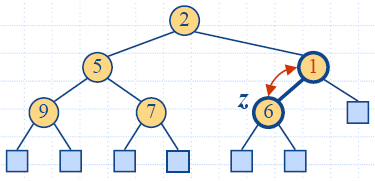
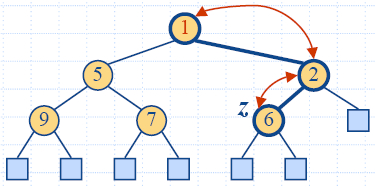
Up-Heap Bubbling after an
Insertion
- After the insertion of a new key k, the heap-order property
may be violated
- Algorithm upheap restores the heap-order property by
swapping k along an upward
path from the insertion node
- Upheap terminates when the key k reaches the root or a node
whose parent has a key smaller than or equal to k
- Since a heap has height O(log
n), upheap runs in O(log n) time
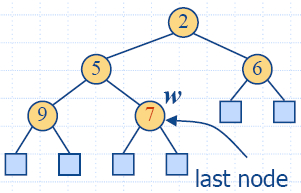
Removal
- Method removeMin
of the priority queue ADT corresponds to
the removal of the root key from the heap
- The removal algorithm consists of three steps
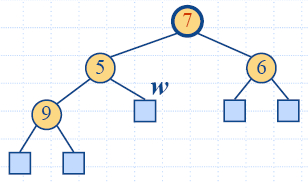
- Replace the root key with the key of the last node w
- Compress w and
its children into a leaf
- Restore the heap-order property (discussed next)
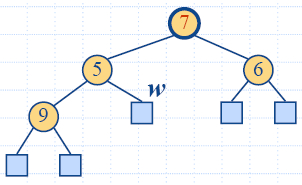
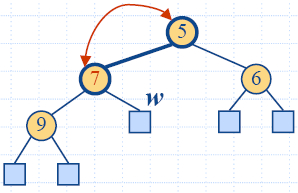
Down-Heap Bubbling after a Removal
- After replacing the root key with the key k of the last node,
the heap-order property may
be violated
- Algorithm downheap restores the heap-order property by
swapping key k along a
downward path from the root
- Downheap terminates when key k reaches a leaf or a node whose
children have keys greater than or equal to k
- Since a heap has height O(log
n), downheap runs in O(log n) time
Analysis
Function
|
Time
|
size(),
isEmpty()
|
O(1)
|
minElement(),
minKey()
|
O(1)
|
insertItem(k,e)
|
O(log n)
|
removeMin()
|
O(log n)
|
7.3.3 C++ Implementation
html-7.7
(HeapTree)
html-7.8 (HPQ1)
html-7.9 (HPQ2)
Heap
Structure Applet Demonstration
Heap
Demonstration
7.3.4 Heap-Sort
- Consider a priority queue with n items implemented by means
of a heap
- the space used is O(n)
- methods insertItem
and removeMin take O(log n) time
- methods size,
isEmpty, minKey, and minElement take O(1) time
- Using a heap-based priority queue, we can sort a sequence of
n elements in O(n
log n) time
- The resulting algorithm is called heap-sort
- Heap-sort is much faster than quadratic sorting algorithms,
such as insertion-sort and selection-sort
Heapsort
Applet