Chapter 6. Trees II
6.3 Binary Trees
A binary tree
is an
ordered tree in which every node has at
most two children. A
binary tree is proper
if each internal node has two children.
 |
- A binary tree is a tree with the following properties:
- Each internal node has two children
- The children of a node are an ordered pair
- We call the children of an internal node left child
and right child
- Alternative recursive definition: a binary tree is
either
- a tree consisting of a single node, or
- a tree whose root has an ordered pair of children,
each of which is a binary tree
|
Examples: arithmetic expression, decision tree
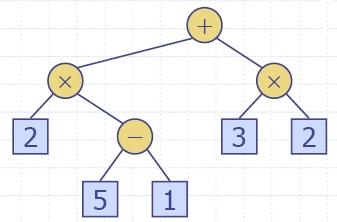
Arithmetic Expression Tree
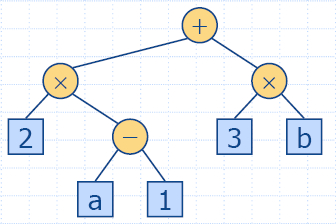
|
- Binary tree associated with
an arithmetic expression
- internal nodes: operators
- external nodes: operands
- Example: arithmetic expression tree for the
expression
(2 × (a
−1) + (3 × b))
|
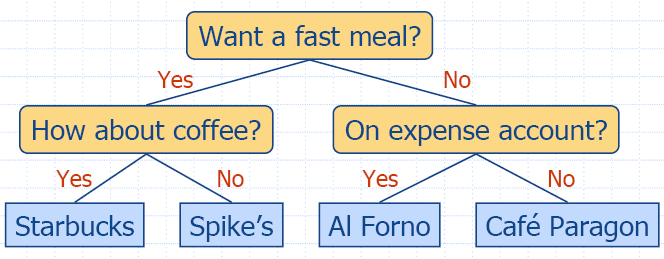
Decision Tree
- Binary tree associated with a decision process
- internal nodes: questions with yes/no answer
- external nodes: decisions
- Example: dining decision
6.3.1 Binary Tree ADT
- The BinaryTree ADT extends the Tree ADT, i.e., it inherits
all the methods of the Tree ADT
- Additional methods:
- Position leftChild(Position);
//error condition for external nodes
- Position rightChild(Position);
//error condition for external nodes
- Position sibling(Position);
// error condition for the root
- Update methods may be defined by data structures
implementing the BinaryTree ADT
6.3.2 A Binary Tree Interface
html-6.14a
(InspectableBinaryTree)
html-6.14b (BinaryTree)
- BinaryTree.cpp
- All functions in the binary tree interface takes O(1) time.
6.3.3 Properties of Binary
Tree
We denote the set of all nodes of a binary tree T, at the same depth d, as the level d of T.
Proposition 6.9: Let T be a proper binary tree with n nodes and let h denote the height of T. Then T has the following properties:
-
The number of external nodes e in T is: h + 1 ≤ e ≤ 2h
-
The number of internal nodes i in T is: h ≤ i ≤ 2h −
1
-
The total number of nodes n
in T is: 2h + 1 ≤ n ≤ 2h+1 − 1
-
The height h of T
is: log2(n + 1) − 1 ≤ h ≤ (n − 1)/2
Proposition 6.10: In a
proper binary tree T,
the number of external nodes e
is 1 more than the number of internal nodes i, i.e. e = i + 1.
Proof. removeAboveExternal(w)
method removes an external node and its parent node.
 |
- Notation
n number of nodes
e number of external
nodes
i number of internal
nodes
h height
-
- Properties:
-
e = i +
1
-
n = 2e − 1
- h ≤ i
-
h ≤ (n − 1)/2
-
e ≤ 2h
-
h ≥
log2e
-
h ≥ log2(n + 1) − 1
|
Traversals of a Binary Tree
Preorder Traversal
of a Binary
Tree
void binaryPreorderPrint(const Tree& T, const Position& v)
{ cout << v.element(); // print element
if (isInternal(v)) // visit children
{ cout << " ";
binaryPreorderPrint(T, T.leftChild(v));
binaryPreorderPrint(T, T.rightChild(v));
}
}
Postorder Traversal of a
Binary
Tree
void binaryPostorderPrint(const Tree& T, const Position& v)
{ if (isInternal(v)) // visit children
{ cout << " ";
binaryPostorderPrint(T, T.leftChild(v));
binaryPostorderPrint(T, T.rightChild(v));
}
cout << v.element(); // print element
}
Evaluating an Arithmetic
Expression
|
- Specialization of a postorder traversal
- recursive method returning the value of a subtree
- when visiting an internal node, combine the values
of the
subtrees
- O(n) time algorithm
|
Algorithm evalExpr(v)
if isExternal (v)
return v.element ()
else
x ← evalExpr(leftChild (v))
y ← evalExpr(rightChild (v))
◊ ← operator stored at v
return x ◊ y |
Inorder Traversal of a Binary
Tree
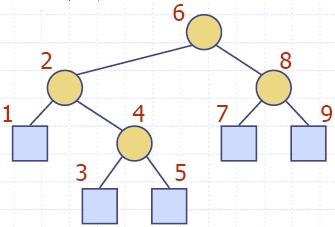 |
- In an inorder traversal a node is visited after its
left
subtree and before its right subtree
- Application: draw a binary tree
- x(v) = inorder rank of v
- y(v) = depth of v
- Visit "left to right"
|
Algorithm inOrder(v)
if isInternal (v)
inOrder(leftChild (v))
visit(v)
if isInternal (v)
inOrder(rightChild (v)) |
void binaryInorderPrint(const Tree& T, const Position& v)
{ if (isInternal(v)) // visit left child
binaryInorderPrint(T, T.leftChild(v));
cout << v.element(); // print element
if (isInternal(v)) // visit right child
binaryInorderPrint(T, T.rightChild(v));
}
Binary
Search Trees
Binary search tree is a binary tree so that
each internal node v stores
an element e, such that:
- the elements stored in the
left subtree of v are less than or equal to e, and
- the elements stored in the right
subtree of v are greater than or equal to e.
Position searchBinaryTree(const Tree& T, const Position& v, const Object& e)
{ if (isInternal(v))
if (v.element() == e) return v; // found!
else if (v.element() < e)
searchBinaryTree(T, T.leftChild(v), e); // search left subtree
else searchBinaryTree(T, T.rightChild(v), e); // search right subtree
else return ... // not found!
}
The time for searching is a binary tree T proportional to the height of T, i.e. >= O(log n) and <= Omega(n).
Examples of creating a BST and searching in a BST.
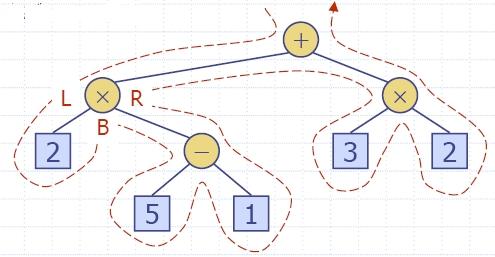
A Unified Tree Traversal
Framework
The Euler Tour Traversal of a
Binary Tree
|
- Generic traversal of a binary tree
- Includes a special cases the preorder, postorder and
inorder
traversals
- Walk around the tree and visit each node three times:
- on the left (preorder)
- from below (inorder)
- on the right (postorder)
|
6.4 Data Structures for Representing Trees
6.4.1 A Vector-Based Structure for Binary Trees
6.4.2 A Linked Structure for Binary Trees
- A node is represented by an object storing
- Element
- Parent node
- Left child node
- Right child node
- Node objects implement the Position ADT
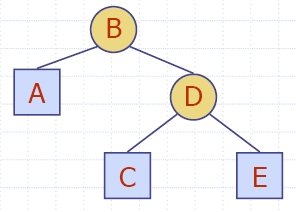
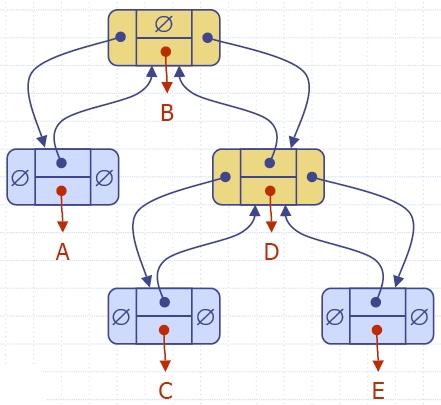
Nodes and Positions in a
Binary Tree
html-6.27 (Node)
html-6.28 (Position)
Binary Tree Update Functions
html-6.29
(LinkedBinaryTree1)
html-6.30
(LinkedBinaryTree2)
LinkedBinaryTree.cpp
Copying a Binary Tree
6.4.3 A Linked Structure for General Trees
- A node is represented by an object storing
- Element
- Parent node
- Sequence of children nodes
- Node objects implement the Position ADT
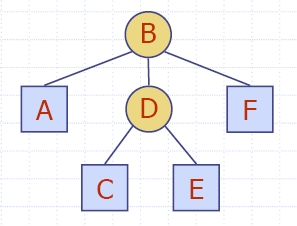
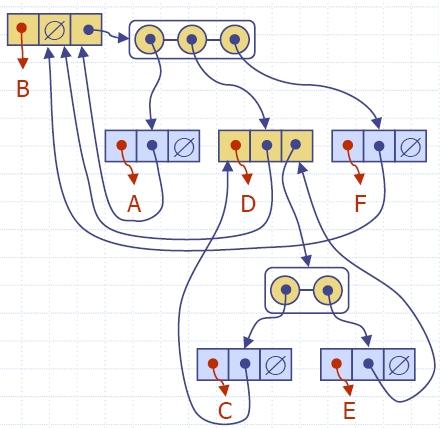
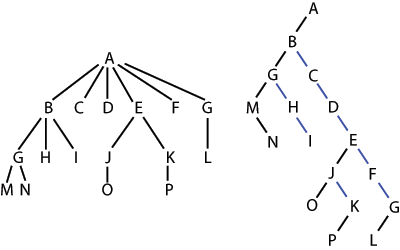
6.4.4 Representing
General
Trees with Binary Trees
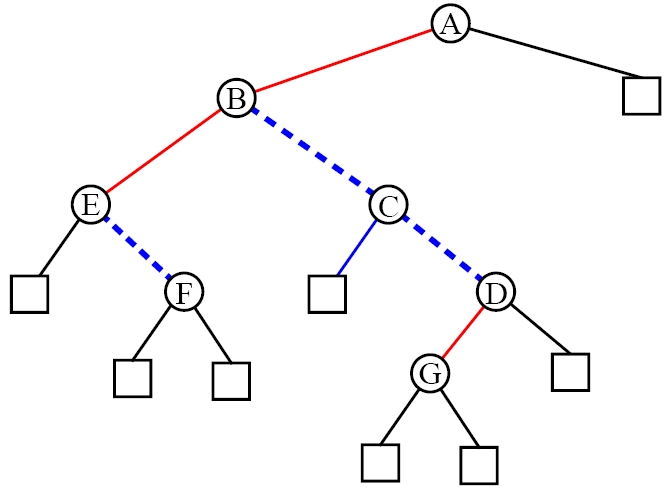
A representation of a general (ordered) tree T is obtained by transforming
T into a binary tree T '. The transformation is as
follows:
- For each node u
of T, there is an internal
node u' of T ' associated with it.
- If u
is an
external node of T and does
not have a sibling immediately following it, then the children of u' are external nodes.
- If u
is an
internal node of T and v is the first child of u in T, then v' if the left child of u' in T '.
- If node v
has a
sibling w immediately
following it, then w' is the
right child of v' in T '.
Additional links:
http://www.cs.purdue.edu/homes/ayg/CS251/slides/chap5.pdf