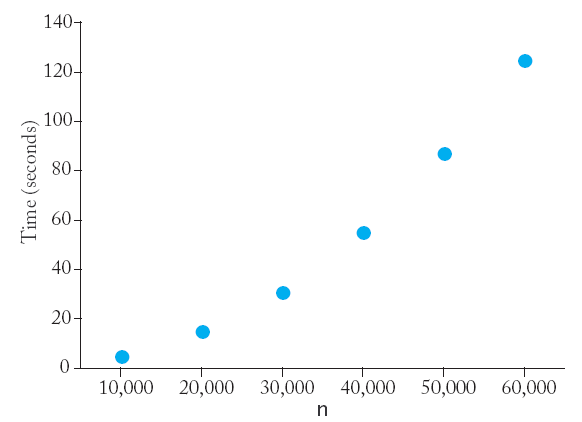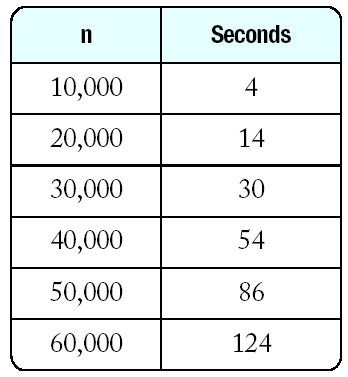
Chapter 15: Sorting and Searching

Chapter Goals

• To compare the selection sort and merge sort algorithms
• To study the linear search and binary search algorithms
• To appreciate that algorithms for the same task can differ widely in performance
• To understand the big-Oh notation
• To learn how to estimate and compare the performance of algorithms
• To learn how to measure the running time of a program.

Selection Sort

• Selection sort is based upon finding the minimum value in a range of indices and placing that value at the front of the vector.
• Example: Suppose we start with the following vector.

  11

  9

  17

  5

  12

• The smallest element is 5, so we place it in the first location in the array. However we cannot lose the 11, so these two elements are swapped.

  5

  9

  17

  11

  12

• Now take the minimum of the remaining entries a[1] ... a[4]. That value is in the correct place, so no swapping is done.

  5

  9

  17

  11

  12

• Repeat the process over the unsorted region.

  5

  9

  11

  17

  12

• Continue until the unprocessed region has length 1. You are done.

  5

  9

  11

  12

  17

Selection Sort (selsort.cpp)

Profiling the Selection Sort Algorithm

• To measure the performance of a program, one could simply run it and measure how long it takes by using a stopwatch.
• Recall that default construction for the Time class initializes the object to the current time.

  Time now

• We can use Time objects to measure the performance of the sorting algorithm.

  Time before;
  selection_sort(v);
  Time after;
  
  cout << "Elapsed time = " << after.seconds_from(before)
       << " seconds\n";
  

• Here are results obtained on a Pentium III processor with a clock speed of 750 MHz running Linux.
• Actually numbers will look different, but the relationship between the numbers will be the same. Doubling the size of the data more than doubles the time needed to sort it.

Analyzing the Performance of the Selection Sort Algorithm

• To analyze the selection sort algorithm, we will count how often an array element is visited.
• For a vector with n elements, we must visit all n of them to find the smallest one. Then visit two elements to swap them.
• In the next step, we visit n - 1 elements to find the minimum, plus two elements to swap.
• In the next step, we visit (n - 2) + 2 elements.
• The total elements visited is

  

  because

  

• The formula for the number of visits in the selection sort algorithm is (1/2) n² + (5/2) n - 3.
• For large values of n, the latter terms in the formula have no significant contribution, so we just ignore them.

  n	(1/2) n2	(5/2) n - 3
  1000	500 000	2 497
  2000	2 000 000	4 997

• When comparing the ratios of counts for different values of n, the coefficient (1/2) cancels out.
• We simply say "The number of visits is of order n²" and use big-Oh notation: The number of visits is O(n²).
• For selection sort, doubling the number of elements increases the time needed for sorting fourfold.
• If a 1000 element vector takes 11 seconds, a 100 000 element vector will require over 3 hours!

Merge Sort

• Suppose you have a vector of 10 integers, with the first and second half already sorted:

  

• It is an easy matter to merge the two sorted halves by taking a new element form either the first or second subvector and choosing the smaller of the elements each time:

  

• If the computer keeps dividing the vector into smaller and smaller subvectors, sorting each half and merging them back together.

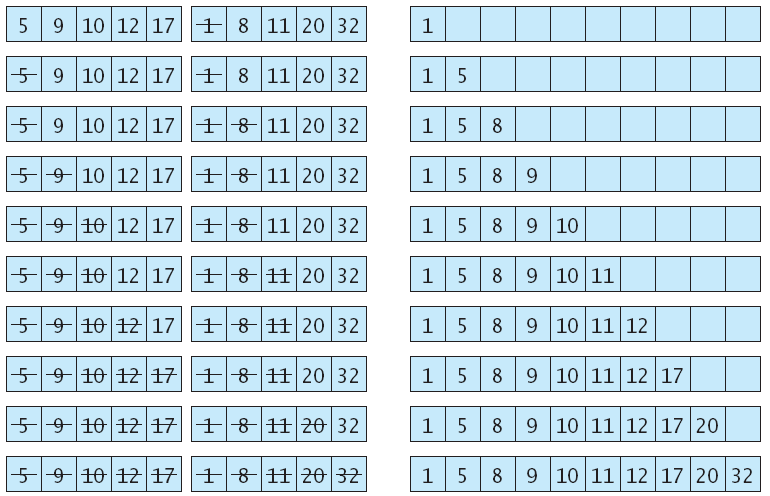
  void merge_sort(vector<int>& a, int from, int to)
  {  if (from == to) return;
     int mid = (from + to) / 2;
     /* sort the first and second half */
     merge_sort(a, from, mid);
     merge_sort(a, mid + 1, to);
     merge(a, from, mid, to);
  }

• The merge procedure discussed in the previous slide then merges the two sorted halves of the vector.

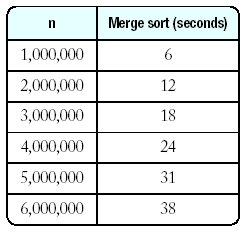
Merge Sort (mergsort.cpp)

Analyzing the Merge Sort Algorithm

• Despite appearing to be a much more complicated algorithm, merge sort performs much better than selection sort.

• Note that the graph does not have a parabolic shape; instead it appears as if running time grows approximately linearly with the size of the array.

• To understand why the merge sort algorithm is such a tremendous improvement, estimate the number of array element visits.
• First we consider the merge process. For a vector of n elements,
  • We must visit the first two elements of the halves and decide which is smaller (2 visits)
  • We must copy the smaller element to it's place in the sorted vector (1 visit)
  • We must copy the sort vector back into the original vector (2 visits)
• So the merge process takes 5n visits.

• To analyze the full algorithm, let T(n) denote the number of visits required to sort a range of n elements through the merge sort process.
• For each of calculation we will assume n = 2^m.
• Because sorting each half will take T(n/2) visits, we have:

  

• A similar analysis yields:

  

• Putting these two results together gives us

  

• Repeating the process gives us:

  

• This analysis generalizes to the formula

  

• Since we assumed n = 2^m we have

  

• To establish growth order, we drop the lower order term and the constant factor.
• The change of base formula for logarithms allows us to drop the base of the logarithm.

  

• Hence merge sort is an O(n log n) algorithm.

• How does O(n²) compare to O(n log n)?
• Recall that it takes 100² = 10 000 times longer to sort 1 000 000 records than it takes to sort 10 000 record with the O(n²) algorithm.
• With the O(n log n) algorithm, the ratio is

  

• If it takes 4 seconds to sort 10 000 records for both sorts (merge sort is really faster, of course) then
  • it will take 10 minutes to merge sort 1 000 000 records
  • it will take 11 hours to selection sort 1 000 000 records

Searching

• If you want to find a number in a sequence of values that occur in arbitrary order, you must look through all elements until you have found a match or until you reach the end.
• This is called a linear or sequential search.
• There is nothing you can do to speed up the search.
• The procedure returns the index of the match, or a -1 if the value cannot be found.

Searching (lsearch.cpp)

Binary Search

• Now search for an item in a data sequence that has been previously sorted.
• Rather than a linear search, we will do a binary search.
• The search is called binary because the size of the search area is cut in half in each step.
• The cutting in half works only because the sequence of values has been sorted.

• Suppose we want to search the following data for 123.

  v[0]	v[1]	v[2]	v[3]	v[4]	v[5]	v[6]	v[7]
  14	43	76	100	115	290	400	511

• The last point in the first half of the data set, v[3], is 100. That means we should look in the second half for a match.

  v[4]	v[5]	v[6]	v[7]
  115	290	400	511

• The last value in the first half of this sequence is 290; hence, the value must be located in the sequence

  v[4]	v[5]
  115	290

• The last value of the first half of this very short sequence is 115, which is smaller than the value we are searching for, so we must look in the second half.

  v[5]

  290

• Since there is only one element, the search easily shows that there is no match.

Binary Search (bsearch.cpp)

• Binary search is a O(log n) algorithm.
• Suppose n = 100, after each search the size of the search range is cut in half to 50, 15, 12, 6, 3, and 1.
  • After seven comparisons we are done.
  • log₂100 is about 6.64386
  • 2⁷ = 128.
• Since binary search is so much faster, is it worthwhile to always sort data before searching?
  • An O(n) search is less work that a O(n log n) sort, so it's not worth it if you only have to perform one search.
  • Sorting first might be worth it if you perform a number of searches of the same vector.

Searching and Sorting Real Data

• Real programs rarely need to search through a collection of integers.
• The procedures above can be modified to easily search through real data.

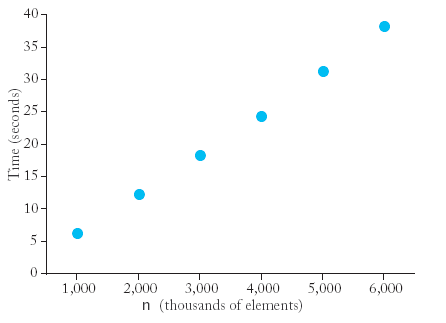  int binary_search(vector<Employee>& v, int from, int to, string n)
  {  if (from > to) return -1;
     int mid = (from + to) / 2;
     if (v[mid].get_name() == n) return mid;
     else if (v[mid].get_name() < n)
        return binary_search(v, mid + 1, to, n);
     else 
        return binary_search(v, from, mid -1 , n);
  }