Курсов проект - INF296
FN
14050
версия 0.1 от
19.06.2003 г.
1.Текст на задачата; използват се
файлов вход и изход.
2. Програма за решаване на задачата - A.CPP, B.CPP, C.CPP Реализиран
са два метода - рекурсия и динамично оптимиране.
Вариант 1
Вариант 2
Вариант
3
3.Файлов вход и изход;
4.Използван е компилатор Dev-C++ 4.9.6.0.
5.Сложност на алгоритмите:
В общия случай алгоритъма е
със сложност O(n.S). Тя зависи едновременно от броя на монетите n и
от общата им стойност S, и можем да я разглеждаме като полиномиална
относно n. Ако М е максималната стойност на монетата измежду
дадените. Тогава: S≤M.n и n.S≤n².M Тогава
сложността на алгоритъма е от порядъка на O(n²), което е многократно
по - добро от O(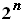 
) при варианта с изчерпване. Когато
времето за работа е квадратично, алгоритъма може да се
използва практически само за малки задачи. Когато
n e хиляда, времето за работа е един милион. Когато n се удвоява,
времето
за работа се увеличава четрикратно. Алгоритъма с експоненциално
нарастване
практически няма приложение, а и прилагането на решения с груба сила
не
е много елегантно. Когато n e двайсет, времето за работа е един
милион.
Когато n се удвои, времето за работа се повдига на квадрат.
n = 10
|
0.000001 сек.
|
n = 100
|
0.0001 сек.
|
n = 1000
|
0.01 сек.
|
n = 10000
|
1.071 сек.
|
n = 100000
|
106.543 сек.
|
n = 1000000
|
10663.6 сек.
|
6. Входен файл
file1.inp с тестови
примери; изходен файл file1.out за примерите от
входния файл.
7. Гранични случаи - входен файл
file2.inp, изходен файл
file2.out.
8. Предложение за:
- входен файл
file3.inp за жури за
състезание по програмиране;
- изходен файл
file3.out за примерите от
входния файл;
- контролно време за работа на програмата за
решаване на примерите - под 1 секунда и за трите примера.
*решенията на рекурсивните
програми не са ефективни за входини файлове с повече от един
пример,тъй като за
прекъсване на рекурсивните
обръщения се използва системната функция ( exit(1) ).
Използвана литература:
1."Основи на компютърните алгоритми" - Преслав
Наков
2."Проектиране и анализ на компютърни алгоритми" - Преслав и Светлин
Накови, Панайот Добриков ( ФМИ, СУ )
3."Алгоритми на 'C' ", Том 1 - Робърт Седжуик