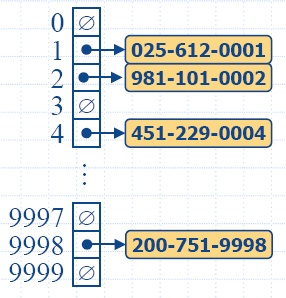
insertItem(5,A)
insertItem(7,B)
insertItem(2,C)
insertItem(8,D)
insertItem(2,E)
find(7)
find(4)
find(2)
findAll(2)
size()
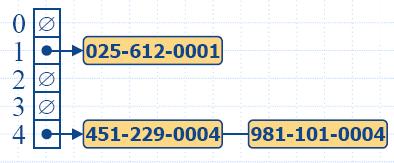
removeElement(5)
removeElement(5)
removeAllElements(2)
find(2)
findAll(2)
|
-
-
-
-
-
p(B)
"null"
p(C) or p(E)
p(C),p(E)
5
-
"error"
-
"null"
"empty iterator"
|
{(5,A)}
{(5,A),(7,B)}
{(5,A),(7,B),(2,C)}
{(5,A),(7,B),(2,C),(8,D)}
{(5,A),(7,B),(2,C),(8,D),(2,E)}
{(5,A),(7,B),(2,C),(8,D),(2,E)}
{(5,A),(7,B),(2,C),(8,D),(2,E)}
{(5,A),(7,B),(2,C),(8,D),(2,E)}
{(5,A),(7,B),(2,C),(8,D),(2,E)}
{(5,A),(7,B),(2,C),(8,D),(2,E)}
{(7,B),(2,C),(8,D),(2,E)}
{(7,B),(2,C),(8,D),(2,E)}
{(7,B),(8,D)}
{(7,B),(8,D)}
{(7,B),(8,D)}
|