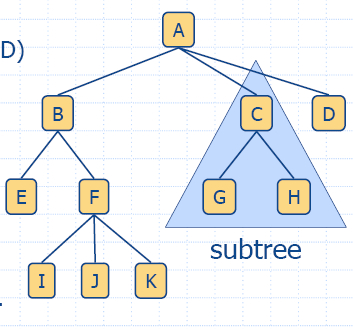
 |
- Root: node without parent (A)
- Internal node: node with at least one child (A,
B,
C, F)
- External node (a.k.a. leaf ): node without
children (E, I, J, K, G, H, D)
- Ancestors of a node (K): parent (F), grandparent
(B),
grand-grandparent (A), etc.
- Depth of a node (F): number of ancestors
(2)
-
Height of a tree: maximum depth
(3) of
any node (J)
- Descendant of a node (A): child (B), grandchild
(F),
grand-grandchild (I), etc.
- Subtree, rooted at a node (C) consists of the
node (C)
and all its descendents (G, H)
|
