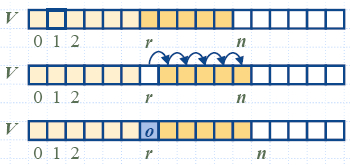
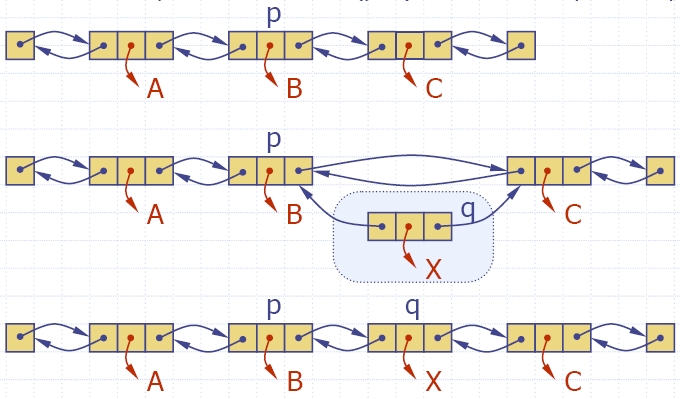
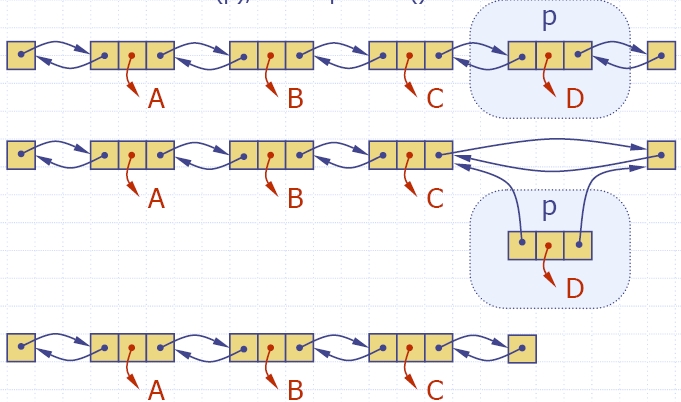
Deletion


| Operation |
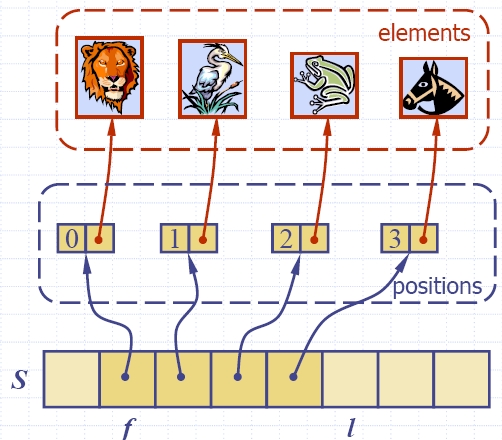
Array |
List |
| size,
isEmpty |
1 |
1 |
| atRank,
rankOf,
elemAtRank |
1 |
n |
| first,
last,
before, after |
1 |
1 |
| replaceElement,
swapElements |
1 |
1 |
| replaceAtRank |
1 |
n |
| insertAtRank,
removeAtRank |
n |
n |
| insertFirst,
insertLast |
1 |
1 |
| insertAfter,
insertBefore |
n |
1 |
| remove |
n |
1 |