 |
 |
|
|
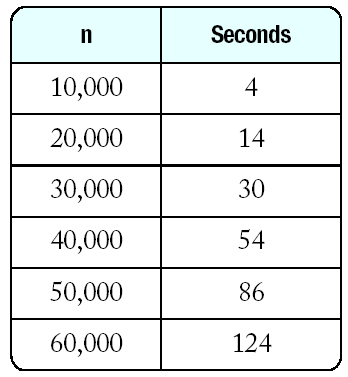
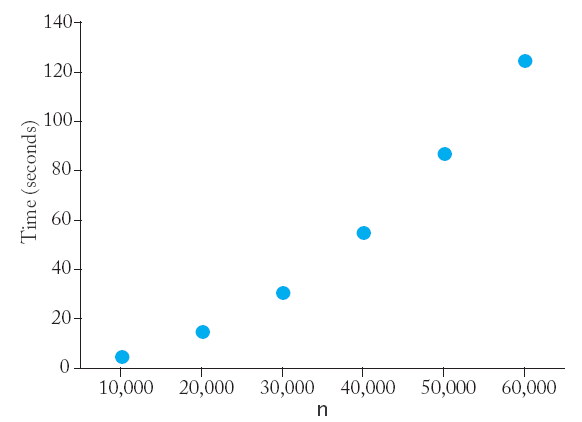
The results obtained on a Intel Core2 CPU T7200 processor with a clock speed of 2 GHz running MS Windows. |
because
Time now
Time before;
selection_sort(v);
Time after;
cout << "Elapsed time = " << after.seconds_from(before)
<< " seconds\n";
 |
 |
|
|
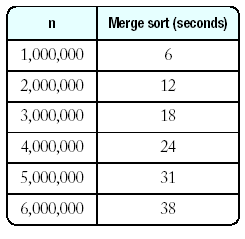
The results obtained on a Intel Core2 CPU T7200 processor with a clock speed of 2 GHz running MS Windows. |
because
void merge_sort(vector<int>& a, int from, int to)
{ if (from == to) return;
int mid = (from + to) / 2;
/* sort the first and second half */
merge_sort(a, from, mid);
merge_sort(a, mid + 1, to);
merge(a, from, mid, to);
}
Merge Sort (mergsort.cpp)
 |
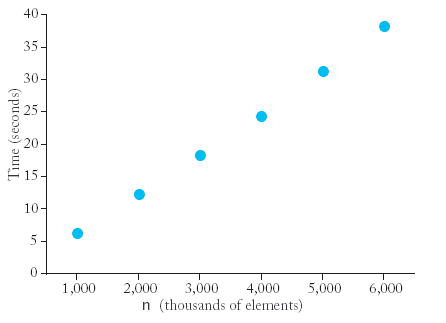 |
| n |
seconds |
| 200000 |
1 |
| 400000 |
2 |
| 800000 |
4 |
| 1600000 |
8 |
| 3200000 |
18 |
|
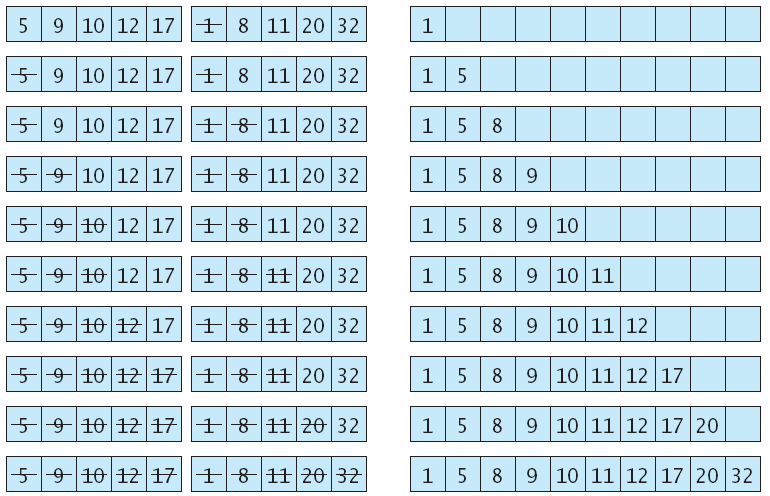
v[5]
|
|
115
|